来源

1. acwing解析视频

   yxc大佬已经讲得很好了，这里只是把图按照自己理解画得形象一点，顺便归纳一下

2. 代码

性质

1. 连续的相同排序操作，只需取最长的那一次进行依次排序即可，不用每次都排序。

   1. 连续的 0 q_i 操作，使[a₁ , a_qi]元素为降序。

      1. 对于其中的任何一次操作j，如果之前的所有操作的区间都比当前的要短（a_qi<=a_qj），则之前所有排序效果可以等效为当前排序中[a₁ , a_qi]部分，[a_qi,a_qj]保持原序不变；
      2. 对于其中的任何一次操作j，如果之后的所有操作的区间都比当前的要短（a_qi>=a_qj），则之后所有排序效果可以等效为当前排序中[a₁ , a_qi]部分，[a_qi,a_qj]保持原降序不变；

   2. 连续的 0 q_i 操作，使[a₁ , a_qi]元素为升序。

      同理可得相似结论。

2. 两种排序操作交替，并且相邻两个排序的范围的重合区间长度越来越短，则每次只需交换重合的区间。

   将研究对象看作重合区间，可以发现重合区间的端点不断地向中间靠拢，并且每一次排序重合区间中的元素都要前后翻转一遍

3. 两种排序操作交替，并且相邻两个排序的范围的重合区间长度越来越长，则只需对最后一次操作排序，并且删除前面两次交替的排序。

符号说明

1. 蓝线：相邻两个排序范围的重合区间范围
2. 箭头：每次排序的区间

图示

建议结合视频一起看

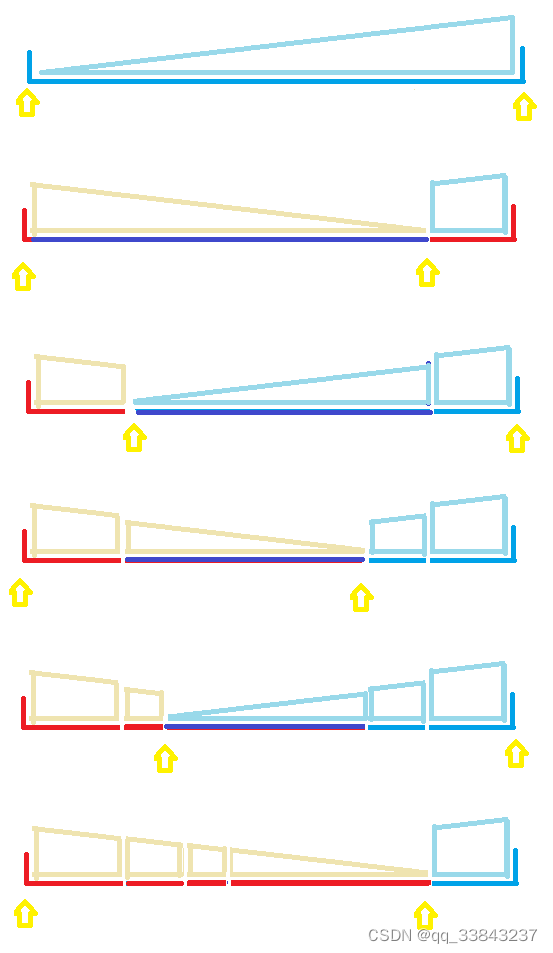
代码

#include 
#include 
#include #define x first
#define y secondusing namespace std;typedef pair PII;const int N = 100010;int n, m;//序列长度，操作次数
PII stk[N];//栈，存储每次操作的操作类型q和参数p
int ans[N];//答案int main()
{scanf("%d%d", &n, &m);int top = 0;while (m -- ){int p, q;//操作类型和参数scanf("%d%d", &p, &q);if (!p)//操作1：a1~aq降序{while (top && stk[top].x == 0) q = max(q, stk[top -- ].y);//出现连续的操作1，我们取q最大（区间最长，性质1.1）while (top >= 2 && stk[top - 1].y <= q) //如果当前的操作1比上一次的操作1范围大，则删除之前的两次排序交替的操作（仅保留最长区间，性质3）top -= 2;stk[ ++ top] = {0, q};//存本次最佳操作}else if (top)//操作2：aq~an升序//&&且操作1已经进行过（操作二第一个用没效果：初始序列是升序的，根据性质1.2，无需再进行一次排序） {while (top && stk[top].x == 1) q = min(q, stk[top -- ].y);//出现连续的操作2，我们取q最小（区间最长，性质1.2）while (top >= 2 && stk[top - 1].y >= q) top -= 2;//如果当前的操作2比上一次的操作2范围大，则删除之前的两次排序交替的操作（仅保留最长区间，性质3）stk[ ++ top] = {1, q};}}//在结果数组里面填数字//枚举每一次操作int k = n, l = 1, r = n;for (int i = 1; i <= top; i ++ ){if (stk[i].x == 0)//操作1：a1~aq降序//右区间左移while (r > stk[i].y && l <= r) ans[r -- ] = k -- ;//移动r值 ，并赋值 else//操作2：aq~an升序//左区间右移while (l < stk[i].y && l <= r) ans[l ++ ] = k -- ; if (l > r) break;//填完了}//若l < r, 表示中间还有些数没有填上（由于有优化，并且询问的次数不一定和元素个数一样）//这个地方不太好理解，建议看图，这里的操作次数top每增加1，排序方式就要改变一次if (top % 2)//操作次数为奇数，则下一次操作为前缀操作，降序填充剩余区间的数while (l <= r) ans[l ++ ] = k -- ;else//操作次数为偶数，则下一次操作为后缀操作，升序填充剩余区间的数while (l <= r) ans[r -- ] = k -- ;for (int i = 1; i <= n; i ++ )printf("%d ", ans[i]);return 0;
}