动态规划(3):价值分配背包问题
创始人
2025-05-30 15:22:00
0次
目录
1.分析
1.1当放入的物品比剩余容量j大时
1.2放的下时
2.代码
1.分析
125 · 背包问题(二) - LintCode
设F(i,j)表示放入i个物品且背包剩余为j容量时的最大价值。
a[]为每个物品的大小,v[]为每个物品的价值,m为最大容量。
状态转移方程为:
1.1当放入的物品比剩余容量j大时
F(i,j)=F(i-1,j);
1.2放的下时
这时,我们需要比较是放入该物品价值更大还是不放入该物品价值更大。
由于我们每次只放入一个物品(即将来矩阵中的元素都是最优解),因此放入物品是取出物品再放入还是直接放入都是相同的结论:
F1(i,j)=F(i-1,j-a[i-1])+v[i-1];
不放入物品的结论和放不下是一样的:
F2(i,j)=F(i-1,j);
最终结论即是从F1和F2取出最大的那个:
F(i,j)=max(F1,F2);
给个图看看吧:
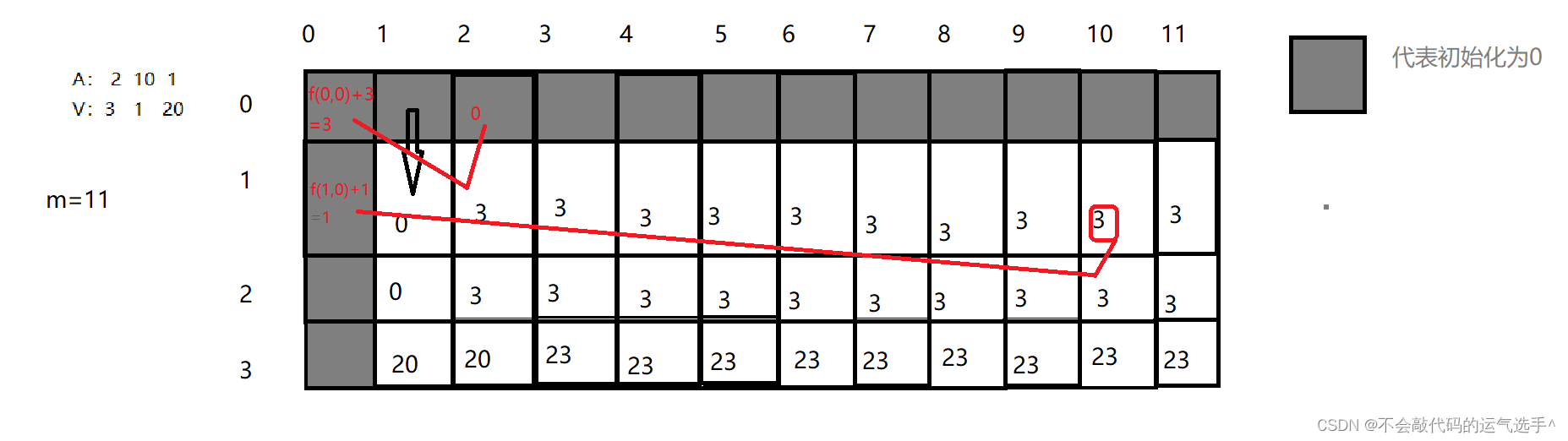
注意:由于防止处理第一个物品或较少容量时越界,我们需要将第一列和第一行初始化为0。
2.代码
int backPackII(int m, vector &a, vector &v) {// write your code herevector> arr;//初始化完成int row=a.size()+1;arr.resize(row);for(int i=0;ij)arr[i][j]=arr[i-1][j];elsearr[i][j]=max((arr[i-1][j-a[i-1]]+v[i-1]),arr[i-1][j]);}}return arr[row-1][m];}
};
相关内容
热门资讯
吉利联手长城围攻比亚迪,下周大...
一周之前长城带头炮轰比亚迪,本周吉利开始呼应长城,联手围攻比亚迪,而且用词更激烈,还是在中国汽车论坛...
防晒指数随意标!“三无”防晒衣...
(央视财经《财经调查》)《财经调查》记者走访发现,市场上标有“防晒”字样的产品品类繁多,但部分防晒衣...
“月入几万,加盟就赚”的快递驿...
很长一段时间里,最受普通人欢迎的创业方式,开奶茶店是一种,加盟快递驿站也是一种。驿站的盛行虽是事实,...
去拉美掘金,月入5万只是及格线...
文 | 严贝贝 陈梓洁编辑 | 曹宾玲数据支持 | 洞见数据研究院半年外派生活结束,大海拿着到手的2...
专访贺铿:既要经济增长,又要低...
本文来源:时代周报 作者:阿力米热2025年是“十四五”规划收官之年,同时也是中国提出“双碳”目标的...
V观财报|若羽臣:朗姿股份计划...
【V观财报|若羽臣:朗姿股份计划减持不超3%公司股份】若羽臣公告,近日收到朗姿股份出具的《关于拟减持...
震惊!宁波某企业公开动员员工当...
“一方面,多名员工离职后因涉职务犯罪被立案或受到刑事处罚;另一方面,公司内部却发邮件鼓励员工报名当‘...
周鸿祎:准备干掉360整个市场...
“ 周鸿祎曾表示自己也想做网红,未来我能够替360节省上10亿元的广告费。从2022年到2024年,...
避雷!A股6月超200家上市公...
大家知道A股有老话:一大涨就减持,很多上市公司敢拉就敢把公司卖给你。最近大家应该能发现每天都有大量上...
汇川技术分拆联合动力上市,关联...
苏州汇川联合动力系统股份有限公司(以下简称“联合动力”)向深交所递交了创业板IPO招股说明书,并且在...
“苏超”热度引爆足球概念,最牛...
过去一周(6月3日—6月6日),三大股指集体上涨。截至6月6日收盘,上证指数周涨幅1.13%,报33...
北交所进入“双指数”投资时代,...
成立近四年的北交所,即将进入“双指数”投资时代。北交所官网最新披露,北交所和中证指数公司将于本月底发...
河南首富换人!泡泡玛特创始人王...
红星资本局6月8日消息,今天上午,根据福布斯实时富豪榜,泡泡玛特(09992.HK)创始人王宁目前身...
罕见一幕发生,银行存款利率跌破...
作者|碎叶冬青近日罕见一幕发生,我们又一次见证了历史。5月20日,六大行宣布下调人民币存款利率,最大...
原则上支持LP冒险|Findm...
各位好,今天录一期。本来是我同事杨博宇写了一篇关于某地政府削减GP管理费的稿子,拿来我发现我有些话想...
今年新股0破发!打新人数创2年...
今年以来,打新人数持续回暖。3月上市的新亚电缆,打新人数超过1400万,是2023年以来的最高值。今...
券商营业部员工卖了1200万基...
红星资本局6月8日消息,一名券商营业部员工在不到一年时间卖出总规模超1200万元的基金产品后,认为公...
利空突袭!集体大跌! 利空突袭...
预期被打得太满,不是好事。据最新消息,标准普尔道琼斯指数公司宣布在最新一轮季度调整中维持标普500指...
一条视频涨粉2000万,韦神凭...
韦东奕为何要开抖音号?01 三句话,涨粉2000万好家伙,还得是韦神。韦东奕最近在抖音上再次创造了一...
美利云初露峥嵘 美利云初露峥嵘...
富凯摘要:数据中心业务已经取得了显著增长。作者|欧文6月6日,3次打开涨停的美利云最终以涨停收盘,股...
