【学习笔记】计算机视觉与深度学习(1.线性分类器)
学习视频:
鲁鹏-计算机视觉与深度学习
1 图像分类任务
图像分类任务是计算机视觉的核心任务,其目标是根据图像信息中所反映的不同特征,把不同类别的图像区分开来。

比如这只狗,我们的目的是给计算机一些选项,比如说猫、狗、飞机、车,让计算机看到这张图片,并得出“这是一只狗”的结论。给出一些猫、飞机、车的图片,机器也能够分类正确。能做到这一点的机器,可以被称作是一种“分类器”。
2 数据驱动的图像分类方法
分为以下三步:
- 数据集构建
- 分类器设计与学习
- 分类器决策
分类器的学习过程图:
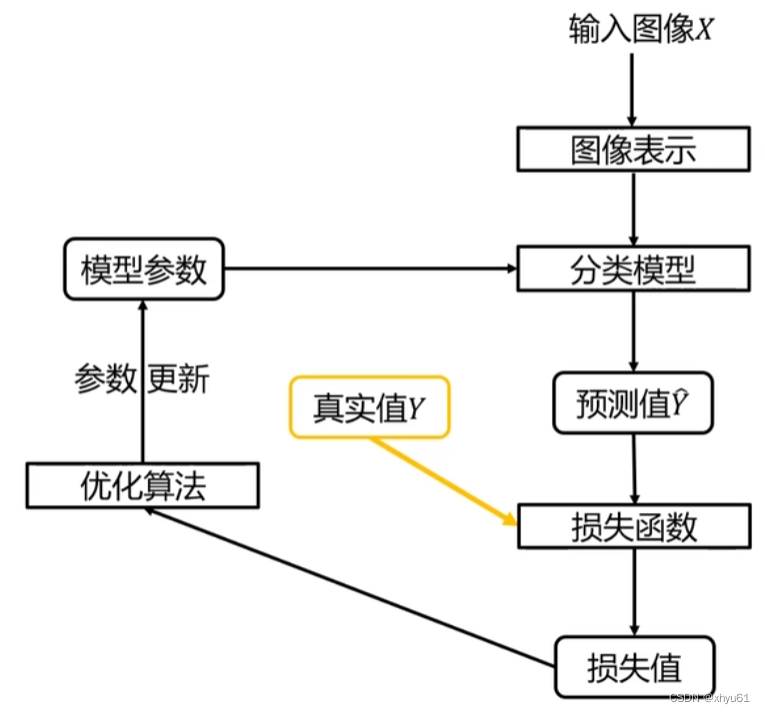
分类器的决策过程图:
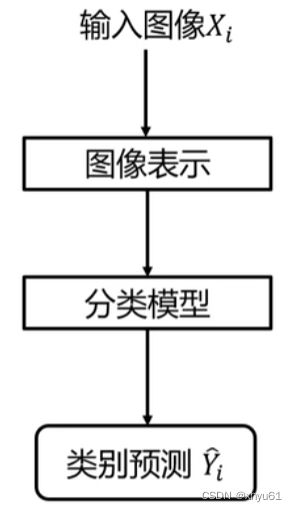
3 图像表示方法
3.1 像素表示
根据RGB的原理,图片中的每一个像素的颜色都可以用一个三元组来表示。假设我们要表示的图像为n×mn\times mn×m的大小的图像,那么就可以用3×n×m3\times n\times m3×n×m维向量来表示这张图像。
3.2 全局特征表示(如GIST)
通过提取整张图像中的全部像素体现出来的特征来表征图像,目的是降低维度。全局提取特征的方法适用于景色类图像的分类,细节较多的分类效果不好。
3.3 局部特征表示(如SIFT)
通过提取整张图像中的部分特征点来表示图像,如人脸识别,识别出两个眼睛一个嘴巴一个鼻子作为特征,这时挡住一个眼睛,也能够做一个较好的判断。同样的场景用于全局特征表示方法,由于其使用所有的像素作为特征提取,去掉一个眼睛会对数据造成很大的变化,导致失败率很高。
4 图像分类任务的评价指标
4.1 正确率与错误率
正确率(accuracy) = 分对的样本数 / 全部样本数
错误率(error rate) = 1 - 正确率
4.2 Top1指标与Top5指标
对于同一张图片,分类器给出其得出的五个最有可能正确的答案,并将他们按照正确的可能性从大到小排序。
Top1指标:可能性最大的答案正确,才被认为分类正确。
Top5指标:可能性最大的五个答案中有正确答案,即被认为分类正确。
5 线性分类器
5.1 图像表示
课程中采用的图像表示方法为像素表示法,将图像的每一个像素的颜色用一个三元组(xi,yi,zi)(x_i, y_i, z_i)(xi,yi,zi)表示,其中0≤xi,yi,zi≤2550\leq x_i, y_i, z_i \leq 2550≤xi,yi,zi≤255。然后将所有点的xi,yi,zix_i,y_i,z_ixi,yi,zi依次排开,假设图像有nnn个点,那么构造一个向量x\mathbf{x}x(本系列笔记中会将代表向量的数学符号像这样加粗):
x=[x0y0z0x1y1z1⋮]\mathbf{x} = \begin{bmatrix} x_0 \\ y_0 \\ z_0 \\ x_1 \\ y_1 \\ z_1 \\ \vdots \end{bmatrix} x=x0y0z0x1y1z1⋮
当所选用的图像是32×3232\times 3232×32时,所得到的x\mathbf{x}x就是一个32×32×3=307232\times 32\times 3=307232×32×3=3072维的向量。
5.2 简介
线性分类器是一种线性映射,将输入的图像特征映射为类别函数。
设x\mathbf{x}x为输入的ddd维图像向量,ccc为类别个数。对于第iii个类别的线性分类器,我们有:
fi(x,wi)=wiTx+bi,i=1⋯cf_i(\mathbf{x},\mathbf{w}_i)=\mathbf{w}_i^T \mathbf{x}+b_i,\ i=1\cdots cfi(x,wi)=wiTx+bi, i=1⋯c
fif_ifi为第iii个类的线性分类器的打分。wi=[wi1wi2⋯wid]T\mathbf{w}_i=\begin{bmatrix} w_{i1} & w_{i2} & \cdots & w_{id} \end{bmatrix} ^Twi=[wi1wi2⋯wid]T是一个列向量表示第iii个类别的权值向量,bib_ibi为偏置。
得到的fif_ifi是一个常数(不难看出,wiT\mathbf{w}_i^TwiT是1×d1\times d1×d的,x\mathbf{x}x是d×1d\times 1d×1的)。
对于每一个类别,都有属于自己的x\mathbf{x}x和bbb。通过公式可以看出,求解分数的这个变换是线性的,所以这个分类器叫做线性分类器。
5.3 决策规则
如果fi(x)>fj(x),∀j≠if_i(\mathbf{x})>f_j(\mathbf{x}), \forall j\neq ifi(x)>fj(x),∀j=i,则决策输入图像x\mathbf{x}x输入第iii类。
其实就是通过线性分类器对这个图像打完分以后,哪一个类别的分数最高,就认为这张图像属于哪一个类别。
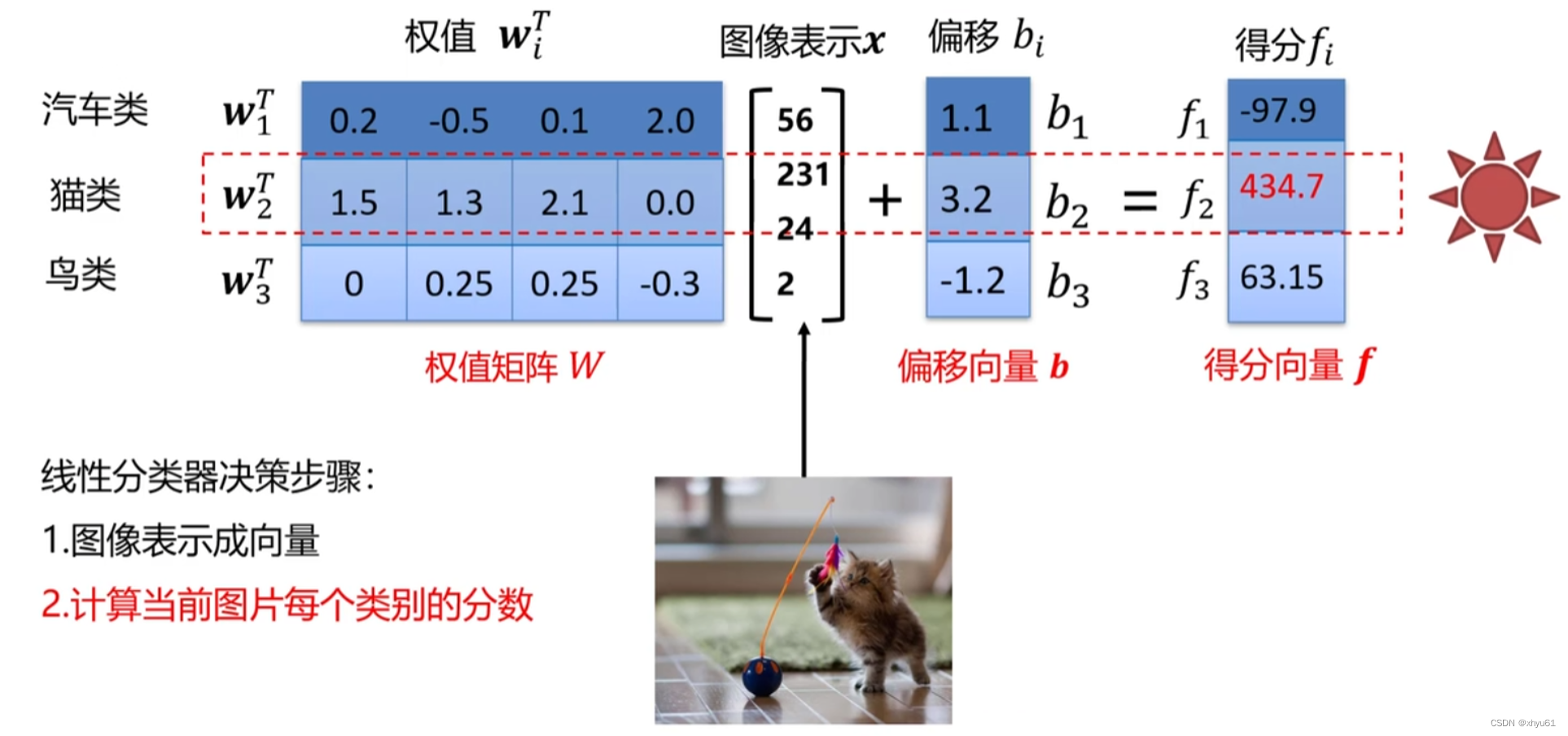
如图所示,将iii个类别的权值向量并到一起可以形成一个权值矩阵W\mathbf{W}W,将每一个类的偏移构成一个便宜向量b\mathbf{b}b,将每一个类最后得到的得分构成一个得分向量f\mathbf{f}f。于是不同于刚刚针对一个类的转移式,我们可以写出一个对于一整个线性分类器的向量转移式:
f(x,W)=Wx+b\mathbf{f}(\mathbf{x},\mathbf{W})=\mathbf{W}\mathbf{x}+\mathbf{b}f(x,W)=Wx+b
5.4 权值
线性分类器的权值可以看做是一个模板,每一个类别通过学习给定的图像,不断调整其中的数值,使其数值更加贴合对应类别的特征。比如说一个具有10个类别的线性分类器,训练后的模板长这个样子:

其模板若隐若现能看出对应类别的图像,但由于是对很多图片的统合学习,所以会出现w8\mathbf{w}_8w8这样子的两个头的马(有的图片马头朝左,有的图片马头朝右导致的)。
输入图像与评估模板的匹配程度越高,分类器输出的分数就越高。
5.5 决策边界
假设我们只用222个特征来表征一个图像,通过画分界面将图片分类开来,大概是这样:
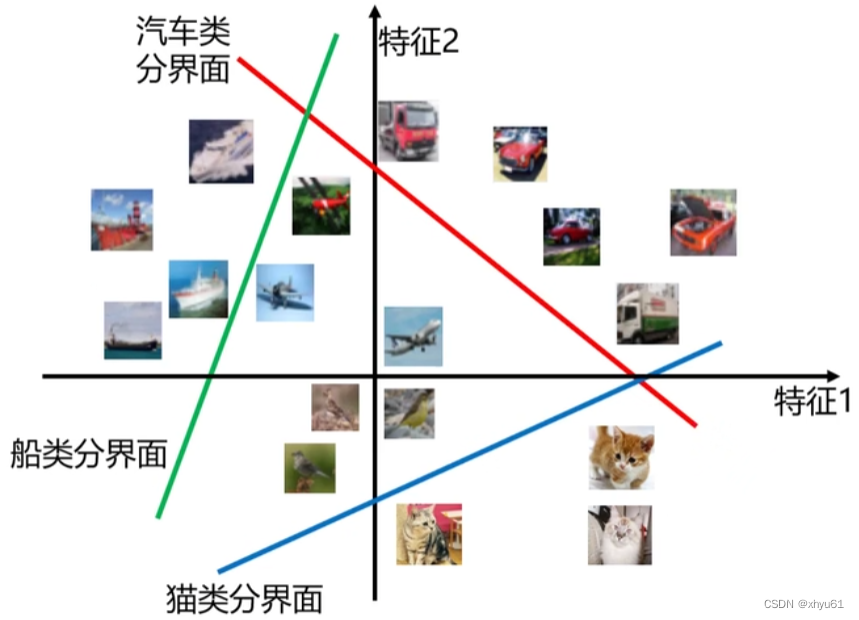
分数为000的线就是分界面,wix+bi=0,i=1⋯c\mathbf{w}_i \mathbf{x}+b_i=0, \ i=1 \cdots cwix+bi=0, i=1⋯c。
因为只有分数大于000,这个图像才有可能为这个类别,假设汽车类分界面,相当于一侧包含所有可能为汽车的图像,而另一侧没有。
我们对线性分类器学习,主要是学习权值矩阵W\mathbf{W}W和偏置向量b\mathbf{b}b,换句话说就是在学习这个分界面。
5.6 损失函数
找到最优的分类模型,还需要损失函数与优化算法的帮忙。我们通过损失函数来判断当前模型的预测情况。具体来说,就是使用测试集对分类器进行测试,观察分类器得出的结果和实际结果的差距,并用损失函数量化表达出来。
损失函数搭建了模型性能和模型参数之间的桥梁,指导模型进行参数优化。具体地说,损失函数是一个函数,用于度量给定分类器的预测值与真实值的不一致程度,其输出通常是一个非负实值。
其输出的非负实值可以作为反馈信号来对分类器参数进行调整,以降低当前示例对应的损失值,提升分类器的分类效果。
损失函数的一般定义
L=1N∑iLi(f(xi,W),yi)L=\frac{1}{N}\displaystyle\sum\limits_{i} L_i(f(\mathbf{x}_i,\mathbf{W}),y_i)L=N1i∑Li(f(xi,W),yi)
其中xix_ixi表示数据集里面第iii张图片;f(xi,W)f(x_i,W)f(xi,W)为分类器对xix_ixi的类别预测;yiy_iyi是该图片的真实类别;LiL_iLi为第iii个样本的预测损失值;LLL为数据集的损失,它是数据集中所有样本损失的平均。
多类支撑向量机损失
sij=fi(xi,wj,bj)=wjTxi+bjs_{ij}=f_i(\mathbf{x}_i,\mathbf{w}_j,b_j)=\mathbf{w}_j^T\mathbf{x}_i+b_jsij=fi(xi,wj,bj)=wjTxi+bj
这个式子中的部分字母和前面所述不同:
jjj:类别标签,取值范围为{1,2,⋯,c}\{1,2,\cdots,c\}{1,2,⋯,c}
wj,bj\mathbf{w}_j, b_jwj,bj:第jjj个类别的权值向量与偏置参数
xi\mathbf{x}_ixi:表示数据集里第iii个样本
sijs_{ij}sij:第iii个样本第jjj类别的预测分数
第iii个样本的多类支撑向量机损失定义如下:
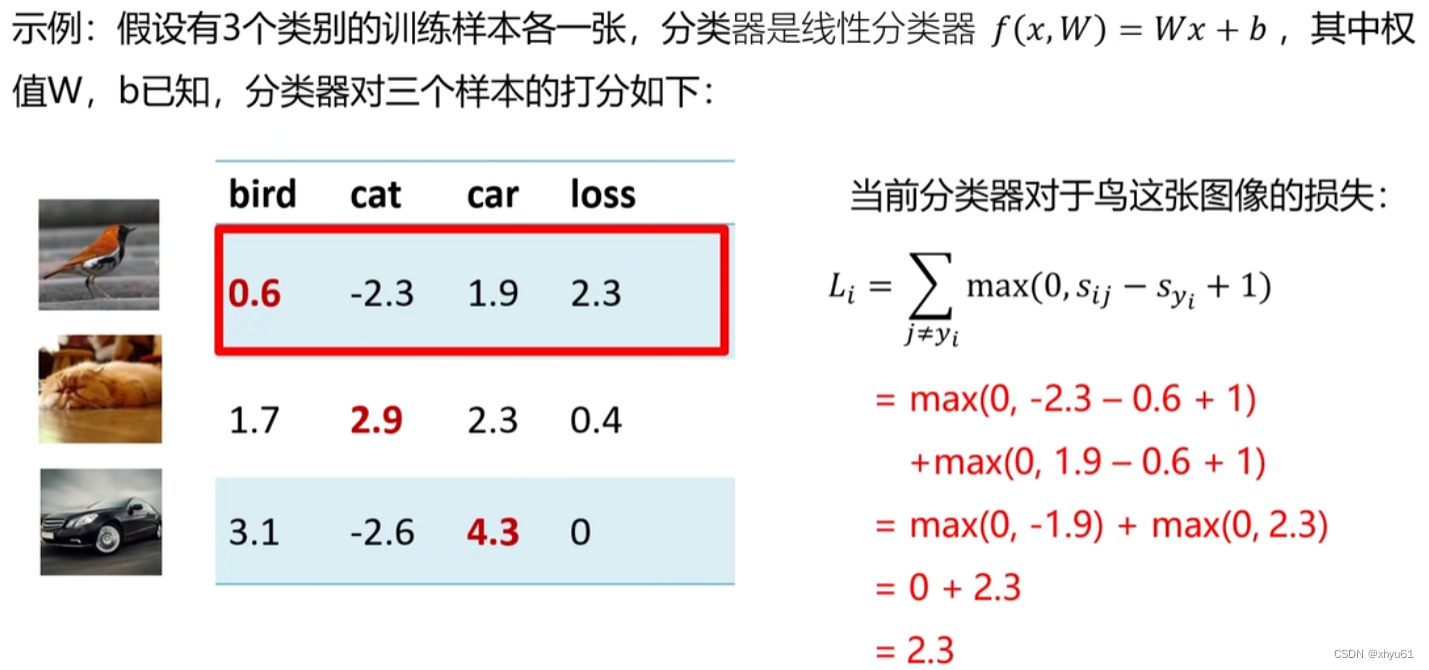
Li=∑j≠yi{0ifsyi≥sij+1sij−syi+1otherwise=∑j≠yimax(0,sij−syi+1)\begin{aligned} L_i &= \displaystyle\sum\limits_{j\neq y_i} \begin{cases} 0 \qquad & if \ s_{y_i}\geq s_{ij}+1 \\ s_{ij}-s_{y_i}+1 \qquad & otherwise \end{cases} \\ &=\displaystyle\sum\limits_{j\neq y_i} \max (0, s_{ij}-s_{y_i}+1) \end{aligned}Li=j=yi∑{0sij−syi+1if syi≥sij+1otherwise=j=yi∑max(0,sij−syi+1)
其中syis_{y_i}syi为第iii个样本真实类别的预测分数。
正确类别的得分比不正确类别的得分高出1分,就没有损失;否则,就会产生损失。
思考:
问 多类支撑向量机损失LiL_iLi的最大/最小值会是多少?
答 预测非常离谱(分值打到了无穷大的极端情况)时预测值可以达到无穷大;完全预测正确时达到最小值000。
问 如果初始化时w\mathbf{w}w和bbb很小,损失LLL会是多少?
答 有ccc个类别时,令w\mathbf{w}w和bbb中的全部权值取000,得到sijs_{ij}sij和syis_{y_i}syi为000,代入式中得到L=c−1L=c-1L=c−1。该特性可以用来检测代码编写是否正确。
问 考虑所有类别(包括j=yij=y_ij=yi),损失LiL_iLi会有什么变化?
答 最终结果会比原来增加111,不会对结果又太大影响,也因此不采用j=yij=y_ij=yi。
问 在总损失LLL计算时,如果用求和代替平均?
答 根据公式,相当于结果乘上NNN,对结果本身不产生影响。
问 如果使用Li=∑j≠yimax(0,sj−syi+1)2L_i= \displaystyle\sum\limits_{j\neq y_i} \max(0,s_j-s_{y_i}+1)^2Li=j=yi∑max(0,sj−syi+1)2?
答 大于111的损失被放大,小于111的损失被缩小,本质上的损失函数会产生一些差异,影响模型优化,可能会出现不同的结果。
问 假设存在一个W\mathbf{W}W使得损失函数L=0L=0L=0,这个W\mathbf{W}W是唯一的吗?
答 不是。
5.7 正则项与超参数
通过5.6节的思考中最后一个问题可以得知,可能会存在多种情况,使得损失函数L=0L=0L=0,这时我们需要用一种方法来判断哪一种更好,或者说找到一种方法去选择。
做法:在损失函数公式后面加入一个正则项。
L=1N∑iLi(f(xi,W),yi)+λR(W)L=\frac{1}{N}\displaystyle\sum\limits_{i} L_i(f(\mathbf{x}_i,\mathbf{W}),y_i)+\lambda R(\mathbf{W})L=N1i∑Li(f(xi,W),yi)+λR(W)
式中λR(W)\lambda R(\mathbf{W})λR(W)为正则项。
其中我们将1N∑iLi(f(xi,W),yi)\frac{1}{N}\displaystyle\sum\limits_{i} L_i(f(\mathbf{x}_i,\mathbf{W}),y_i)N1i∑Li(f(xi,W),yi)称作数据损失,模型预测需要和训练集相匹配;将λR(W)\lambda R(\mathbf{W})λR(W)称作正则损失,防止模型在训练集上学习得“太好”。
R(W)R(\mathbf{W})R(W)是一个与权值有关,跟图像无关的函数。
λ\lambdaλ是一个超参数,控制着正则损失在总损失中所占的比重。
超参数
超参数是学习过程之前设置的参数,而不是学习中得到的。超参数一般都会对模型的性能有重要的影响。
观察
L=1N∑iLi(f(xi,W),yi)+λR(W)L=\frac{1}{N}\displaystyle\sum\limits_{i} L_i(f(\mathbf{x}_i,\mathbf{W}),y_i)+\lambda R(\mathbf{W})L=N1i∑Li(f(xi,W),yi)+λR(W)
当λ=0\lambda = 0λ=0时,优化结果仅与数据损失相关。
当λ=∞\lambda = \inftyλ=∞时,优化结果与数据损失无关,仅考虑权重损失。此时,系统最优解为W=0\mathbf{W}=\mathbf{0}W=0。
L2正则项
R(W)=∑k∑lWk,l2R(\mathbf{W})=\displaystyle\sum\limits_{k}\displaystyle\sum\limits_{l} W_{k, l}^2R(W)=k∑l∑Wk,l2
举例说明

L2正则损失对大数值权值进行惩罚,喜欢分散数值,鼓励分类器将所有维度的特征都用起来,而不是强烈的依赖其中少数几维特征。
正则项让模型有了偏好!
常用的正则项
L1正则项:R(W)=∑k∑l∣Wk,l∣R(\mathbf{W})=\displaystyle\sum\limits_{k}\displaystyle\sum\limits_{l} |W_{k, l}|R(W)=k∑l∑∣Wk,l∣
L2正则项:R(W)=∑k∑lWk,l2R(\mathbf{W})=\displaystyle\sum\limits_{k}\displaystyle\sum\limits_{l} W_{k, l}^2R(W)=k∑l∑Wk,l2
Elastic net(L1+L2):R(W)=∑k∑lβWk,l2+∣Wk,l∣R(\mathbf{W})=\displaystyle\sum\limits_{k}\displaystyle\sum\limits_{l} \beta W_{k, l}^2 + |W_{k, l}|R(W)=k∑l∑βWk,l2+∣Wk,l∣
5.8 参数优化
参数优化是机器学习的核心步骤之一,它利用损失函数的输出值作为反馈信号来调整分类器参数,以提升分类器对训练样本的预测性能。
损失函数L=1N∑i=1NLi+λR(W)L=\frac{1}{N}\displaystyle\sum\limits_{i=1}^N L_i + \lambda R(\mathbf{W})L=N1i=1∑NLi+λR(W),是一个与参数W\mathbf{W}W有关的函数,优化的目标是找到使损失函数LLL达到最优的那组参数W\mathbf{W}W。
有直接方法:∂L∂W=0\frac{\partial L}{\partial W}=0∂W∂L=0
但由于LLL形式一般很复杂,很难求解,因此提出梯度下降算法。
梯度下降算法
梯度下降算法是一种简单而高效的迭代优化算法。
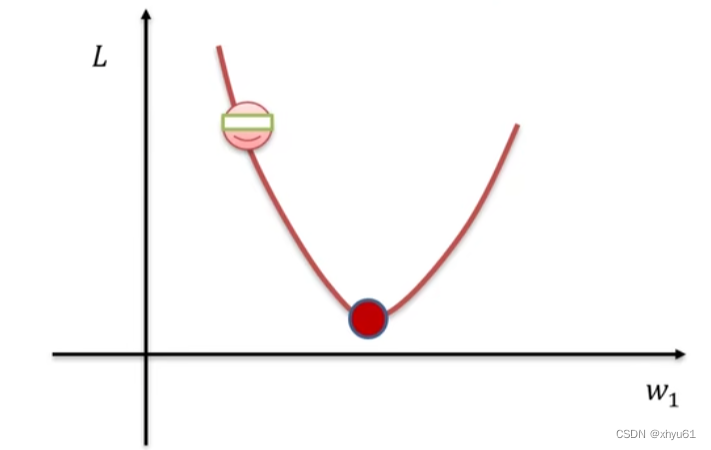
如图所示,红色点左上角的蒙上眼睛的笑脸是我们当前的位置。假设当前我们在LLL函数的图像上遇到了一个极值点,我们通过一点一点向着往下的坡的方向去移动。于是有两个问题:
- 往哪儿走?——负梯度方法
- 要走多远?——步长来决定
梯度下降:利用所有样本计算损失并更新梯度。
while true权值的梯度 ← 计算梯度(损失、训练样本、权值)权值 ← 权值 - 学习率 * 权值的梯度
数值法
一维变量,函数求导:
dL(w)dw=limh→0L(w+h)−L(w)h\frac{dL(w)}{dw}=\displaystyle\lim\limits_{h\rightarrow 0} \frac{L(w+h)-L(w)}{h}dwdL(w)=h→0limhL(w+h)−L(w)
解析法
示例:损失函数L(w)=w2L(w)=w^2L(w)=w2,求w=1w=1w=1点处的梯度。
∇L(w)=2w\nabla L(w)=2w∇L(w)=2w
∇w=1L(w)=2\nabla_{w=1} L(w)=2∇w=1L(w)=2
解析法精确、快速,但是导数函数推导易错。
一般求解梯度使用解析法,通过数值法验证(梯度检查)。
如何计算多类支撑向量机损失的导数函数?
Li=∑j≠yimax(0,sij−syi+1)L_i= \displaystyle\sum\limits_{j\neq y_i} \max(0,s_{ij}-s_{y_i}+1)Li=j=yi∑max(0,sij−syi+1)
将sij=wjTxi+bjs_{ij}=\mathbf{w}_j^T \mathbf{x}_i +b_jsij=wjTxi+bj代入上式,得到:
Li=∑j≠yimax(0,wjTxi+bj−wyiTxi+byi+1)L_i= \displaystyle\sum\limits_{j\neq y_i} \max(0,\mathbf{w}_j^T \mathbf{x}_i +b_j-\mathbf{w}_{y_i}^T \mathbf{x}_i +b_{y_i}+1)Li=j=yi∑max(0,wjTxi+bj−wyiTxi+byi+1)
现尝试通过解析法求解,我们先以简单例子入手:假设y=max(0,w2−1)y=\max(0, w^2-1)y=max(0,w2−1),那么有
∂y∂w={2wifw2−1≥00otherwise\frac{\partial y}{\partial w}= \begin{cases} 2w \qquad & if \ w^2-1 \geq 0 \\ 0 \qquad & otherwise \end{cases} ∂w∂y={2w0if w2−1≥0otherwise
同理,对于我们要求的∂Li∂wj\frac{\partial L_i}{\partial \mathbf{w}_j}∂wj∂Li,也可以分段:
当wjTxi+bj−wyiTxi+byi+1<0\mathbf{w}_j^T \mathbf{x}_i +b_j-\mathbf{w}_{y_i}^T \mathbf{x}_i +b_{y_i}+1<0wjTxi+bj−wyiTxi+byi+1<0时,有∂Li∂wj=0\frac{\partial L_i}{\partial \mathbf{w}_j}=0∂wj∂Li=0。
当wjTxi+bj−wyiTxi+byi+1≥0\mathbf{w}_j^T \mathbf{x}_i +b_j-\mathbf{w}_{y_i}^T \mathbf{x}_i +b_{y_i}+1\geq0wjTxi+bj−wyiTxi+byi+1≥0时,有∂Li∂wj=xi\frac{\partial L_i}{\partial \mathbf{w}_j}=\mathbf{x}_i∂wj∂Li=xi。这个导数涉及到了矩阵求导,推导过程如下:
观察LiL_iLi式中只有wjTxi\mathbf{w}_j^T \mathbf{x}_iwjTxi这一项与wj\mathbf{w}_jwj有关,其他的都可以忽略不计,于是我们可以把LiL_iLi的式子(仅在求导时)看作:
Li=wjTxi=xi1wj1+xi2wj2+⋯+xidwjdL_i=\mathbf{w}_j^T \mathbf{x}_i=x_{i1}w_{j1}+x_{i2}w_{j2}+\cdots + x_{id}w_{jd}Li=wjTxi=xi1wj1+xi2wj2+⋯+xidwjd
根据矩阵求导,我们有
∂Li∂wj=[∂Liwj1∂Liwj2⋮∂Liwjd]=[xi1xi2⋮xid]=xi\frac{\partial L_i}{\partial \mathbf{w}_j}= \begin{bmatrix} \frac{\partial L_i}{w_{j1}} \\ \frac{\partial L_i}{w_{j2}} \\ \vdots \\ \frac{\partial L_i}{w_{jd}} \\ \end{bmatrix}= \begin{bmatrix} x_{i1} \\ x_{i2} \\ \vdots \\ x_{id} \\ \end{bmatrix}=\mathbf{x}_i ∂wj∂Li=wj1∂Liwj2∂Li⋮wjd∂Li=xi1xi2⋮xid=xi
所以我们有:
∂Li∂wj={xiifwjTxi+bj−wyiTxi+byi+1≥00otherwise\frac{\partial L_i}{\partial \mathbf{w}_j}= \begin{cases} \mathbf{x}_i \qquad & if \ \mathbf{w}_j^T \mathbf{x}_i +b_j-\mathbf{w}_{y_i}^T \mathbf{x}_i +b_{y_i}+1\geq0 \\ 0 \qquad & otherwise \end{cases} ∂wj∂Li={xi0if wjTxi+bj−wyiTxi+byi+1≥0otherwise
而∂Li∂bj\frac{\partial L_i}{\partial b_j}∂bj∂Li较好求,不多说明:
∂Li∂bj={1ifwjTxi+bj−wyiTxi+byi+1≥00otherwise\frac{\partial L_i}{\partial b_j}= \begin{cases} 1 \qquad & if \ \mathbf{w}_j^T \mathbf{x}_i +b_j-\mathbf{w}_{y_i}^T \mathbf{x}_i +b_{y_i}+1\geq0 \\ 0 \qquad & otherwise \end{cases} ∂bj∂Li={10if wjTxi+bj−wyiTxi+byi+1≥0otherwise
利用这些已求导数,我们可以求出L(W)L(\mathbf{W})L(W)的梯度。
L(W)=1N∑i=1NLi(xi,yi,W)+λR(W)L(\mathbf{W})=\frac{1}{N}\displaystyle\sum\limits_{i=1}^N L_i(x_i, y_i, \mathbf{W}) + \lambda R(\mathbf{W})L(W)=N1i=1∑NLi(xi,yi,W)+λR(W)
∇WL(W)=1N∑i=1N∇WLi(xi,yi,W)+λ∇WR(W)\nabla_\mathbf{W} L(\mathbf{W})=\frac{1}{N}\displaystyle\sum\limits_{i=1}^N \nabla_\mathbf{W}L_i(x_i, y_i, \mathbf{W}) + \lambda \nabla_\mathbf{W}R(\mathbf{W})∇WL(W)=N1i=1∑N∇WLi(xi,yi,W)+λ∇WR(W)
while true权值的梯度 ← 计算梯度(损失、训练样本、权值)权值 ← 权值 - 学习率 * 权值的梯度
不难发现,当NNN很大时,权值的梯度所需的计算量很大。
随机梯度下降算法
每次随机选择一个样本xix_ixi,计算损失并更新梯度。
L(W)=Li(xi,yi,W)+λR(W)L(\mathbf{W})=L_i(x_i, y_i, \mathbf{W}) + \lambda R(\mathbf{W})L(W)=Li(xi,yi,W)+λR(W)
∇WL(W)=∇WLi(xi,yi,W)+λ∇WR(W)\nabla_\mathbf{W} L(\mathbf{W})= \nabla_\mathbf{W}L_i(x_i, y_i, \mathbf{W}) + \lambda \nabla_\mathbf{W}R(\mathbf{W})∇WL(W)=∇WLi(xi,yi,W)+λ∇WR(W)
while true数据 ← 从训练数据采样(训练数据, 1)权值的梯度 ← 计算梯度(损失, 训练样本, 权值)权值 ← 权值 - 学习率 * 权值的梯度
但是单个样本的训练可能会带来很多噪声,不是每次迭代都向着整体最优化的方向。
小批量梯度下降算法
每次随机选取mmm个(批量的大小,也是一个超参数)个样本,计算损失并更新梯度。
L(W)=1m∑i=1mLi(xi,yi,W)+λR(W)L(\mathbf{W})=\frac{1}{m}\displaystyle\sum\limits_{i=1}^m L_i(x_i, y_i, \mathbf{W}) + \lambda R(\mathbf{W})L(W)=m1i=1∑mLi(xi,yi,W)+λR(W)
∇WL(W)=1m∑i=1N∇WLi(xi,yi,W)+λ∇WR(W)\nabla_\mathbf{W} L(\mathbf{W})=\frac{1}{m}\displaystyle\sum\limits_{i=1}^N \nabla_\mathbf{W}L_i(x_i, y_i, \mathbf{W}) + \lambda \nabla_\mathbf{W}R(\mathbf{W})∇WL(W)=m1i=1∑N∇WLi(xi,yi,W)+λ∇WR(W)
一些名词的介绍(会实现的代码中)
iteration:表示1次迭代,每次迭代更新1次网络结构的参数;
batch_size:1次迭代所使用的样本量;
epoch:1个epoch表示过了1遍训练集中的所有样本。
通常使用2的幂数作为批量大小,比如说32或64或128个样本。
while true小批量数据 ← 从训练数据采样(训练数据, 批量大小)权值的梯度 ← 计算梯度(损失, 小批量数据, 权值)权值 ← 权值 - 学习率 * 权值的梯度
6 数据集
6.1 数据集划分
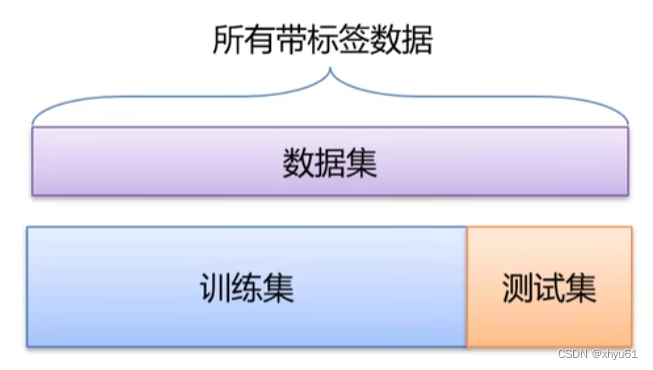
训练集→训练模型,寻找最优的分类器;
测试集→评估模型,评测泛化能力。
问 如果模型含有超参数(比如正则化强度),如何找到泛化能力最好的超参数?
答 再设立一个验证集,用于选择超参数。
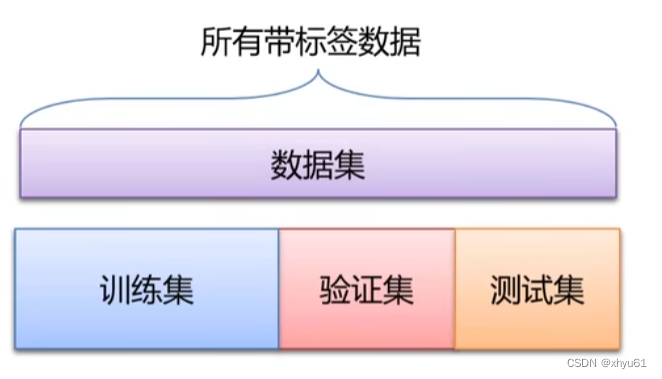
训练集用于给定的超参数时分类器参数的学习;
验证集用于选择超参数;
测试集评估泛化能力。
(这样可以避免训练过程中看到测试集,使得出现过拟合现象)
问 如果数据很少,那么可能验证集包含的样本就很少,从而无法在统计上代表数据。
这个问题很容易发现,如果在划分数据前进行不同的随机打乱,最终得到的模型性能差别很大,那么就存在这个问题。
K折交叉验证
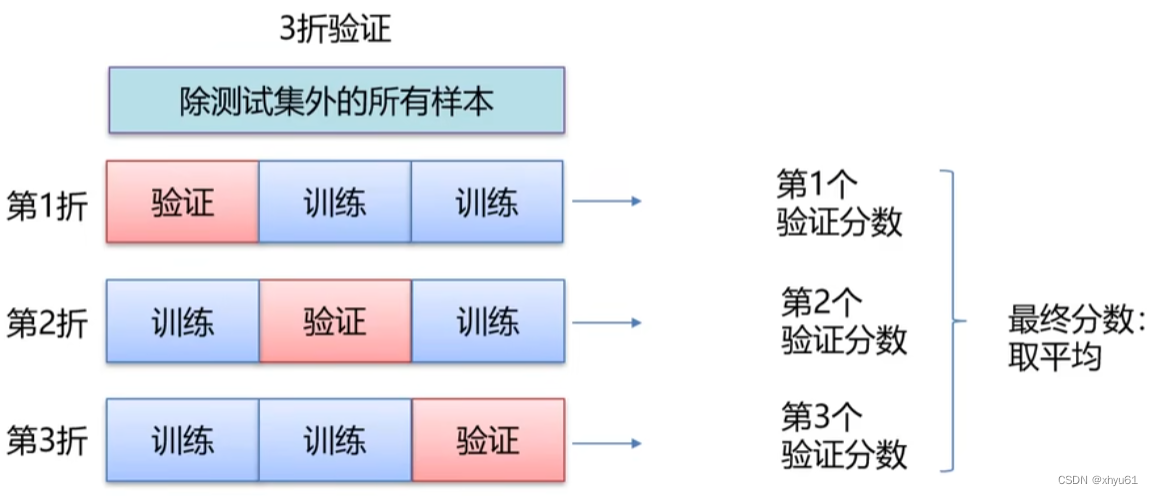
带打乱顺序的K折交叉验证
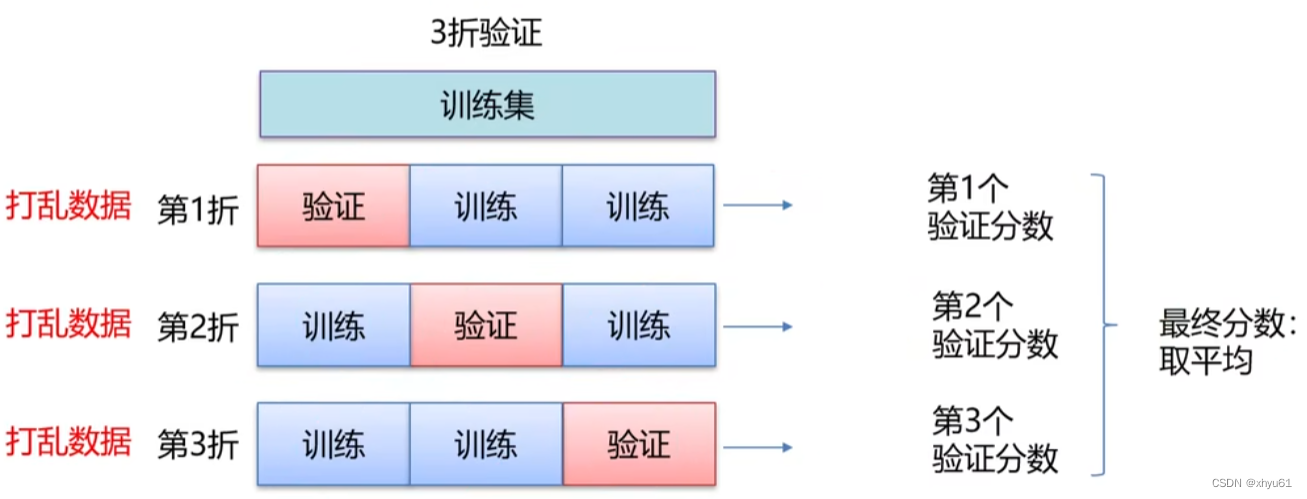
6.2 数据预处理
数据能否直接使用?有哪些处理方式?

通常不太会直接使用原始数据进行学习。
假设原始数据中的数据分别为xix_ixi,均值为xˉ\bar{x}xˉ,最小值为min(x)\min(x)min(x),最大值为max(x)\max(x)max(x),标准差为σ(x)\sigma(x)σ(x)。
去均值的方法:xi←xi−xˉx_i \leftarrow x_i-\bar{x}xi←xi−xˉ。
归一化的方法有两种:
- min-max归一化:xi←xi−min(x)max(x)−min(x)x_i \leftarrow \frac{x_i-\min(x)}{\max(x)-\min(x)}xi←max(x)−min(x)xi−min(x)
- mean归一化:xi←xi−xˉmax(x)−min(x)x_i \leftarrow \frac{x_i-\bar{x}}{\max(x)-\min(x)}xi←max(x)−min(x)xi−xˉ
标准化的方法:xi←xi−xˉσ(x)x_i \leftarrow \frac{x_i-\bar{x}}{\sigma(x)}xi←σ(x)xi−xˉ
事实上,归一化和标准化都是把数据图像中心平移到原点。但是归一化没有改变数据分布的形状,而标准化使样本数据的分布近似为某种分布(通常为正态分布)。
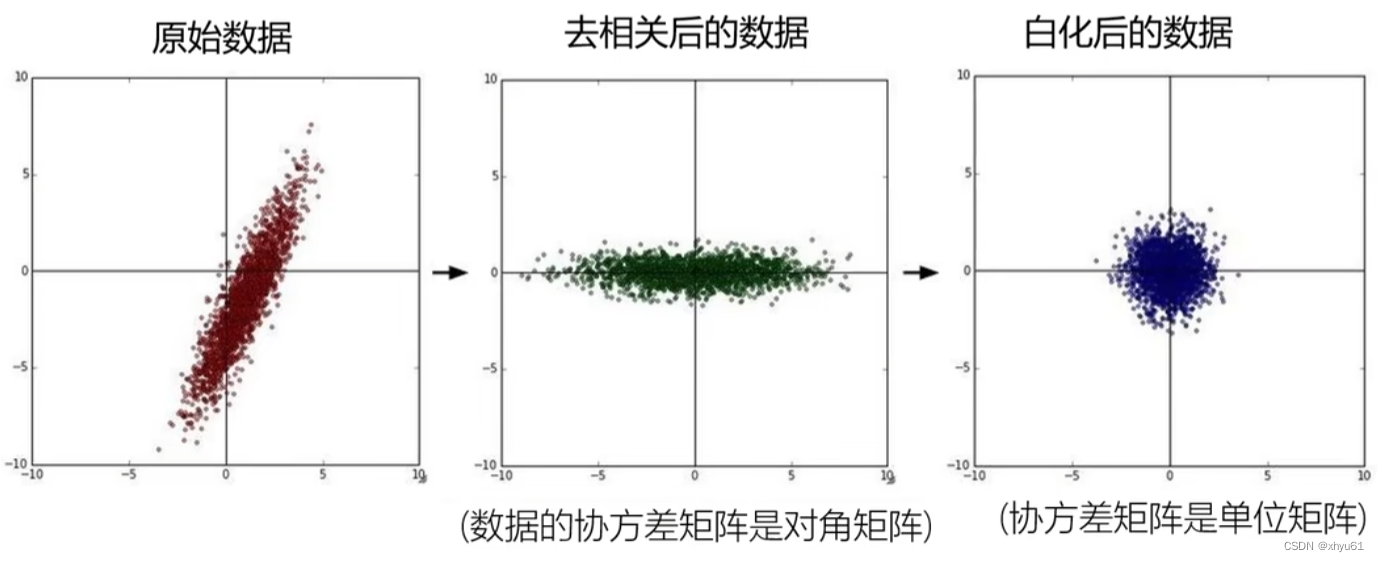
原始数据中可以看出,xxx增大时,yyy也有总体增大的趋势,所以我们可以认为此时xxx和yyy是相关的。但学习的过程中,我们不希望把xxx和yyy两种东西放在一起去考虑,这时我们采取去相关的操作。去相关后,可以看出yyy的变化方式与xxx没有关系了。如此一来,我们可以把xxx和yyy分开单独考虑,实现“降维”的效果。
白化为去相关后进行标准化。
神经网络中用到更多的是去均值和标准化、归一化。
