文章目录

• 介绍
• SDNE
• • 问题定义
  • 框架
  • 损失函数
• 实验
• • 数据集和超参
  • 图重建
  • 多标签分类
  • 链路预测
  • 可视化
  • 参数敏感性
• 总结

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。

介绍

Wang D, Cui P, Zhu W. Structural deep network embedding[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 1225-1234.

网络无处不在，许多现实世界中的应用程序都需要挖掘网络中的信息。比如社交网络中推荐好友，在网络集群用户并推荐商品，在蛋白质网络中研究分子等，挖掘网络中的信息是非常重要的。

一个有效的方法就是将网络嵌入到一个低维空间，然后通过学习到的嵌入向量对网络进行重建，也就是用图嵌入的方法学习网络的表示。

但是学习网络表示面临着以下3个挑战：

1. 高度非线性化
   网络中的潜在结构是高度非线性的，因此设计模型来捕捉这种高度非线性的结构是很困难的。
2. 如何保留结构
   网络中潜在结构是非常复杂的，节点间的相似性依赖局部和全局网络架构，如何同时保留局部和全局结构也是一个棘手的问题。
3. 稀疏性问题
   许多真实世界的网络是高度稀疏的，仅利用非常有限的观察到的边不足以达到令人满意的性能。

对于上述三个问题，SDNE分别提出了解决方法：
设计一个深度模型来学习网络中的节点表示，包含多个非线性函数的多层架构，可以将数据映射到高度非线性的潜在空间，从而能够捕获高度非线性的网络结构。
利用一阶临近度和二阶临近度来解决如何保留结构和稀疏性问题，利用一阶临近度和二阶临近度可以分别保留局部和全局网络结构，为此同时保留二者，提出了一个半监督框架来学习表示。

此外，如图1所示，节点间的二阶临近度的数量是远远多于一阶临近度的，因此二阶临近度可以提供更多的信息来描述网络结构。

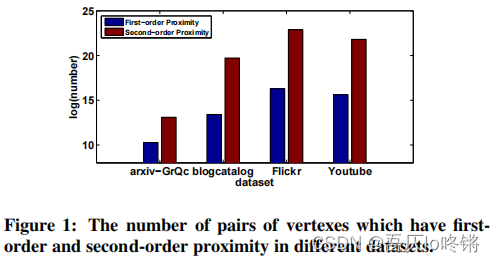
总的来说，SDNE贡献如下：

1. 一个结构化深度网络嵌入方法，称为SDNE。可以将数据映射到一个高度非线性潜在空间来保留网络结构，并且对于系数网络也具有鲁棒性。
2. 一个新的半监督深度模型，同时利用了一阶临近度和二阶临近度，来保留局部和全局网络结构。
3. 通过实验表明了SDNE的优越性。

SDNE

问题定义

• 图（Graph）
  定义图G=(V,E)G=(V,E)G=(V,E)，其中V=v1,...,vnV={v_1,...,v_n}V=v1​,...,vn​表示n个节点，E={ei,j}i,j=1nE={\{e_{i,j}\}}^n_{i,j=1}E={ei,j​}i,j=1n​表示边，其中每条边的权重为si,js_{i,j}si,j​，若节点间不存在边则si,j=0s_{i,j}=0si,j​=0；若存在边，对于无权重图si,j=1s_{i,j}=1si,j​=1，对于有权重图si,j>1s_{i,j}>1si,j​>1。

• 一阶临近度（First-Order Proximity）
  对于任何一对节点，若si,j>0s_{i,j}>0si,j​>0则表明节点viv_ivi​和节点vjv_jvj​之间存在一阶临近度，否则不存在一阶临近度。也就是看邻接矩阵中具体值，一节邻近度描述了两节点是否相连，是否存在边。

• 二阶临近度（Second-Order ）
  给定Nu={su,1,...,su,∣v∣}N_u=\{s_{u,1},...,s_{u,|v|}\}Nu​={su,1​,...,su,∣v∣​}表示节点uuu和其他节点的一阶临近度，节点uuu和节点vvv间二阶临近度则是NuN_uNu​和NvN_vNv​的相似性。也就是比较邻接矩阵中的两行，二阶临近度描述了两节点有多少共同邻居。

• 图嵌入（Network Embedding）
  图嵌入旨在学习一个映射函数f:vi→yi∈Rdf:v_i→y_i\in\R^df:vi​→yi​∈Rd，其中d<<∣V∣d<<|V|d<<∣V∣。也就是从高维映射到低维，映射过程称为嵌入，得到映射结果为嵌入向量。

框架

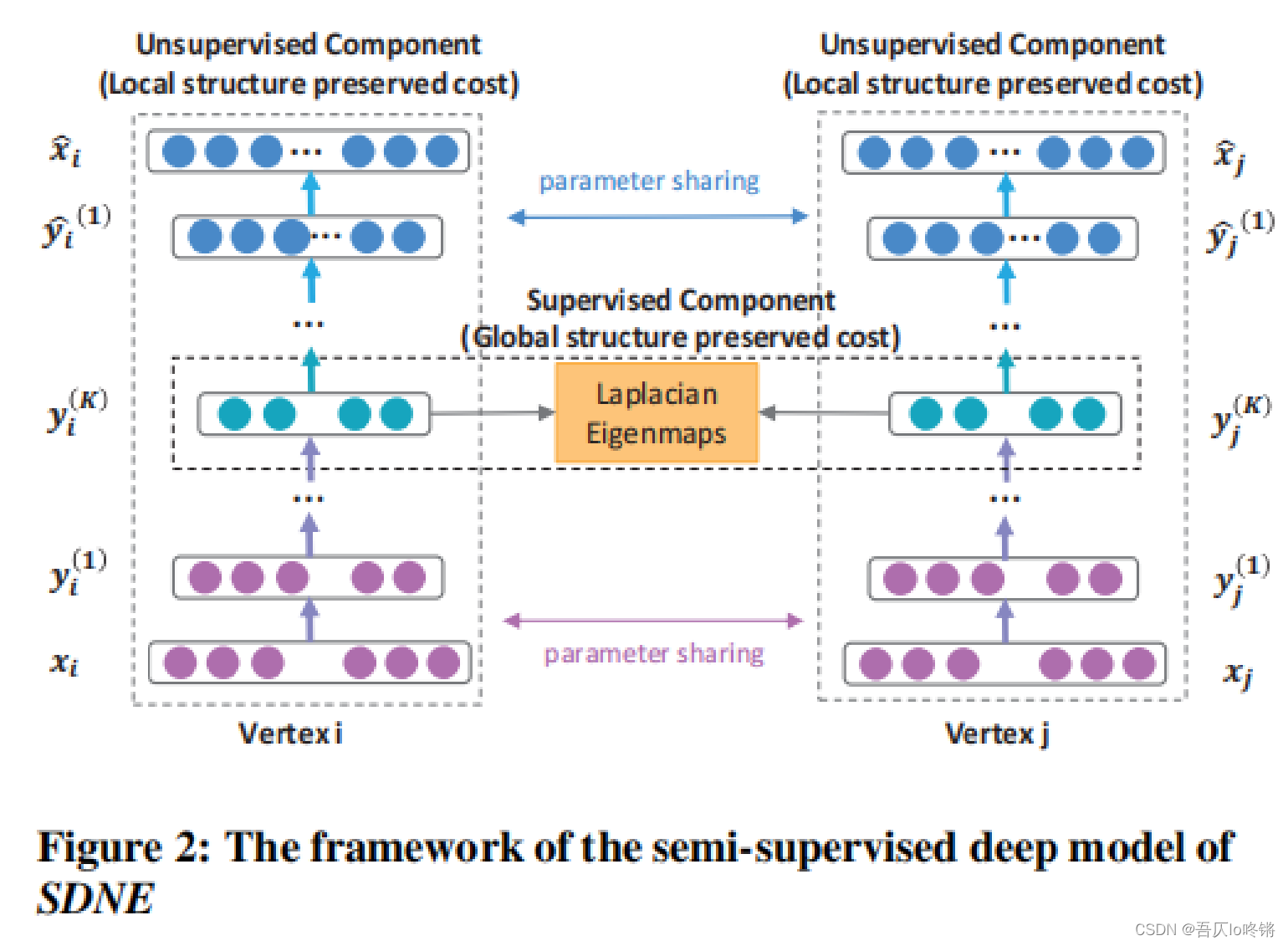
SDNE模型是一个半监督深度学习模型。

对于节点iii的输入特征xix_ixi​（邻接矩阵第iii行），经过KKK层全连接层的编码器（隐含层神经元个数递减），嵌入到一个低维空间，得到嵌入向量yi(K)y_i^{(K)}yi(K)​，然后再经过KKK层的全连接层的解码器（与编码器相反且一一对应），学习到解码后节点iii的新特征表示。自编码器中是用的非监督损失函数，最优化二阶临近度，保留全局结构特征（我怀疑图片上标错了）。

对于两个节点iii和jjj，对拉普拉斯特征值映射进行扩展，使用监督损失函数，最优化一阶临近度，保留局部结构特征。

通过联合优化一阶邻近度和二阶临近度，同时保留图的局部和全局结构特征。下面介绍具体损失函数定义。

损失函数

• 一阶临近度损失
  使用一阶临近度来保留网络的局部特征，作为监督信息来约束一对顶点的潜在表示的相似性。
  L1st=∑i,j=1nsi,j∣∣yi−yj∣∣22\mathcal{L}_{1st}=\sum_{i,j=1}^ns_{i,j}{||y_i-y_j||}^2_2L1st​=i,j=1∑n​si,j​∣∣yi​−yj​∣∣22​
  idea源于拉普拉斯特征值映射，当相似节点在嵌入空间中映射得较远时给予惩罚。使由一条边连接的顶点映射到嵌入空间后相近。

• 二阶临近度损失
  使用二阶临近度来保留网络的全局特征，使有更多相同邻居的节点映射到嵌入空间后更相近。但是直接使用邻接矩阵作为传统自编码器的输入，将更倾向于重建邻接矩阵中的零元素。而这并不是我们所期待的，因此提高了重建非零元素的惩罚权重，如下所示：
  L2nd=∣∣(X^−X)⊙B∣∣F2\mathcal{L}_{2nd}={||(\hat{X}-X)\odot B||}^2_FL2nd​=∣∣(X^−X)⊙B∣∣F2​
  其中，bi={bi,j}j=1nb_i={\{b_{i,j}\}}^n_{j=1}bi​={bi,j​}j=1n​，当si,j=0,bi,j=1s_{i,j}=0,b_{i,j}=1si,j​=0,bi,j​=1，否则bi,j=β>1b_{i,j}=\beta>1bi,j​=β>1。也就是重建非零元素的权重β>1\beta>1β>1大于重建零元素的权重，避免学习到全是0矩阵，以及稀疏矩阵数据不平衡情况。换句话说，如果一个数据集是全连接的话就不需要BBB了。

• 正则化损失
  预防过拟合的情况。
  Lreg=12∑k=1K(∣∣W(k)∣∣F2+∣∣W^(k)∣∣F2)\mathcal{L}_{reg}=\frac{1}{2}\sum_{k=1}^K({||W^{(k)}||}^2_F+{||\hat{W}^{(k)}||}^2_F)Lreg​=21​k=1∑K​(∣∣W(k)∣∣F2​+∣∣W^(k)∣∣F2​)

• 最终损失
  最终损失函数，联合优化一阶邻近度和二阶临近度。
  Lmix=L2nd+αL1st+vLreg\mathcal{L}_mix=\mathcal{L}_{2nd}+\alpha \mathcal{L}_{1st}+v\mathcal{L}_{reg}Lm​ix=L2nd​+αL1st​+vLreg​

实验

数据集和超参

使用了5个数据集，各个数据集中节点和边情况如下表所示：

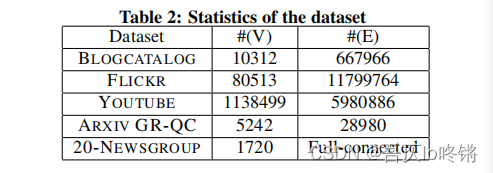
自编码器中隐含层神经元数量设置：

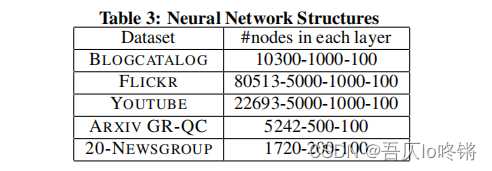
但是比较关键的超参数α、β、v\alpha、\beta、vα、β、v使用了网格搜索，原文并没有公开。参考一些开源库中取值α=1e−2,β=5,v=1e−2\alpha=1e-2,\beta=5,v=1e-2α=1e−2,β=5,v=1e−2，但是自己写论文跑实验的话还是免不了网格搜索这步。

图重建

图重建任务顾名思义就是根据原图输入，经过模型学习编码和解码后得到新的图表示，以此来评估是否是一个好的图嵌入算法，因为一个好的图嵌入算法的嵌入向量可以保留原图的网络结构。

使用precision@k(i)precision@k(i)precision@k(i)和MAPMAPMAP来作为评价指标：
precision@k(i)=∣{j∣i,j∈V,index(j)≤k,Δi(j)=1}∣kprecision@k(i)=\frac{|\{j|i,j\in V,index(j)\leq k,\Delta_i(j)=1\}|}{k}precision@k(i)=k∣{j∣i,j∈V,index(j)≤k,Δi​(j)=1}∣​
AP(i)=∑jprecision@j(i)⋅Δi(j)∣{Δi(j)=1}∣AP(i)=\frac{\sum_jprecision@j(i)·\Delta_i(j)}{|\{\Delta_i(j)=1\}|}AP(i)=∣{Δi​(j)=1}∣∑j​precision@j(i)⋅Δi​(j)​
MAP=∑i∈QAP(i)∣Q∣MAP=\frac{\sum_{i\in Q}AP(i)}{|Q|}MAP=∣Q∣∑i∈Q​AP(i)​
precision@kprecision@kprecision@k中，index(j)index(j)index(j)是排序后的第jjj个顶点，Δi(j)=1\Delta_i(j)=1Δi​(j)=1表示节点viv_ivi​和vjv_jvj​之间存在一条边。precision@k(i)precision@k(i)precision@k(i)表示对于第iii个顶点，学习到的图表示中，最有可能相连的前kkk个顶点中（也就是对学习到的邻接矩阵第iii行排序），有多少个是原图中和节点iii相连的。

AP(i)AP(i)AP(i)表示节点iii的平均精度，也就是对于不同的KKK值情况求平均。但是注意只考虑有边的情况，也就是说原图中节点iii和kkk间存在边，才加上该项precision@k(i)，分母也是有边的数量。

MAPMAPMAP表示所有查询的平均精度，这里的查询可以是对所有节点，也可以是采样部分节点进行计算。

实验结果如下表所示：

分析：

• 在以上两个数据集中，SDNE在MAP指标上比其他基线算法有显著提高。
• 尽管SDNE和LINE都利用了一阶邻近度和二阶临近度来保留图结构，但SDNE取得了更好的效果，这是因为LINE采用浅层模型架构(shallow structure)，而SDNE采用深度自编码器。此外，LINE是分别优化，而SDNE是联合优化一阶和二阶临近度。
• SDNE和LINE的表现都比LE好，而LE仅利用了一阶临近度。（说明了二阶邻近度的重要性）

（插播反爬信息 ）博主CSDN地址：https://wzlodq.blog.csdn.net/

多标签分类

分类任务在许多应用和相关算法中是至关重要的，通过图嵌入算法学习的的图表示（即嵌入向量）被当作输入特征来对节点进行多标签分类。

采用了LIBLINEAR开源库作为分类器，将数据集按比例随机划分为训练集和测试集，并采用F1指标来衡量分类结果，其定义如下：
Macro−F1=∑A∈CF1(A)∣C∣Macro-F1=\frac{\sum_{A\in C}F1(A)}{|C|}Macro−F1=∣C∣∑A∈C​F1(A)​
Pr=∑A∈CTP(A)∑A∈C(TP(A)+FP(A))Pr=\frac{\sum_{A\in C}TP(A)}{\sum_{A\in C}(TP(A)+FP(A))}Pr=∑A∈C​(TP(A)+FP(A))∑A∈C​TP(A)​
R=∑A∈CTP(A)∑A∈C(TP(A)+FN(A))R=\frac{\sum_{A\in C}TP(A)}{\sum{A\in C}(TP(A)+FN(A))}R=∑A∈C(TP(A)+FN(A))∑A∈C​TP(A)​
Micro−F1=2∗Pr∗RPr+RMicro-F1=\frac{2*Pr*R}{Pr+R}Micro−F1=Pr+R2∗Pr∗R​

F1对召回率和准确率进行权衡，考量分类器查得全不全和查得准不准，值越大则表明分类效果越好。


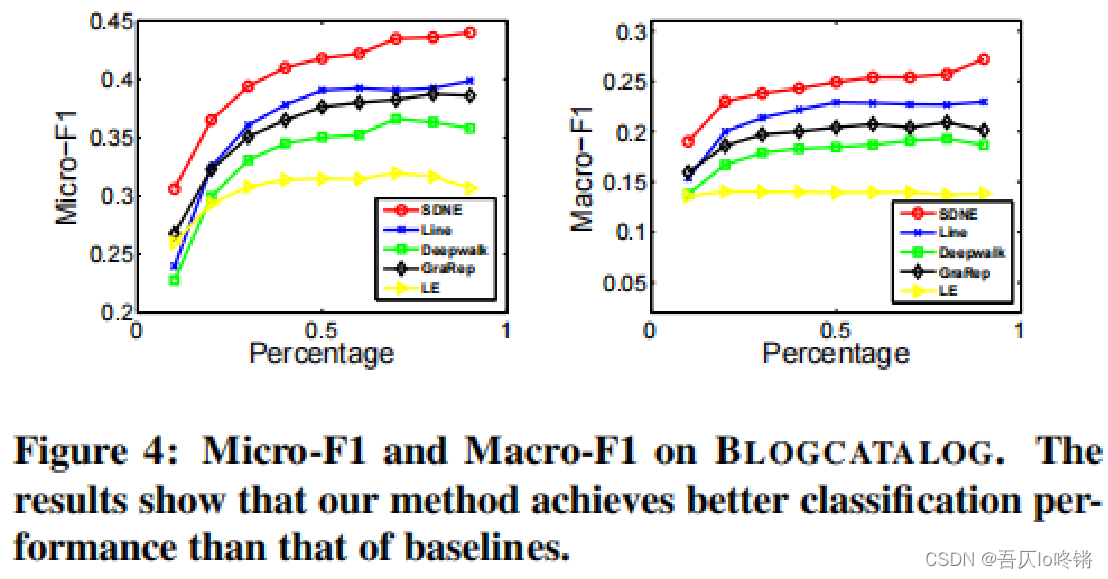
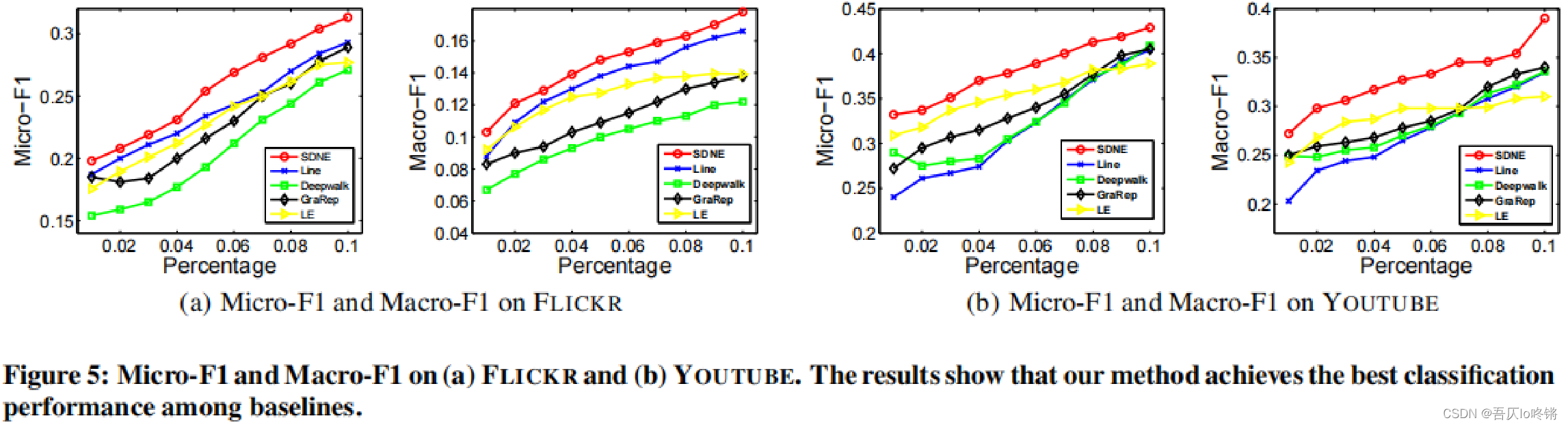
分析：

• 在上面的三个数据集中，SDNE的F1指标始终高于其他方法。SDNE学习到的嵌入向量可以很好的保留图的结构，并服务于下游任务，如作为分类器的输入特征。

链路预测

实际应用中，我们只是观察到了网络中的部分链路（边），仍有相当一部分的链路是未被观察到的，或是未来可能出现的新链路。因此链路预测在应用中也是一个重要的任务。

链路预测的评价指标也是precision@k、AP和MAPprecision@k、AP和MAPprecision@k、AP和MAP，也就是预测的前KKK个链路中，有多少是原图中实际存在和观察到的链路。

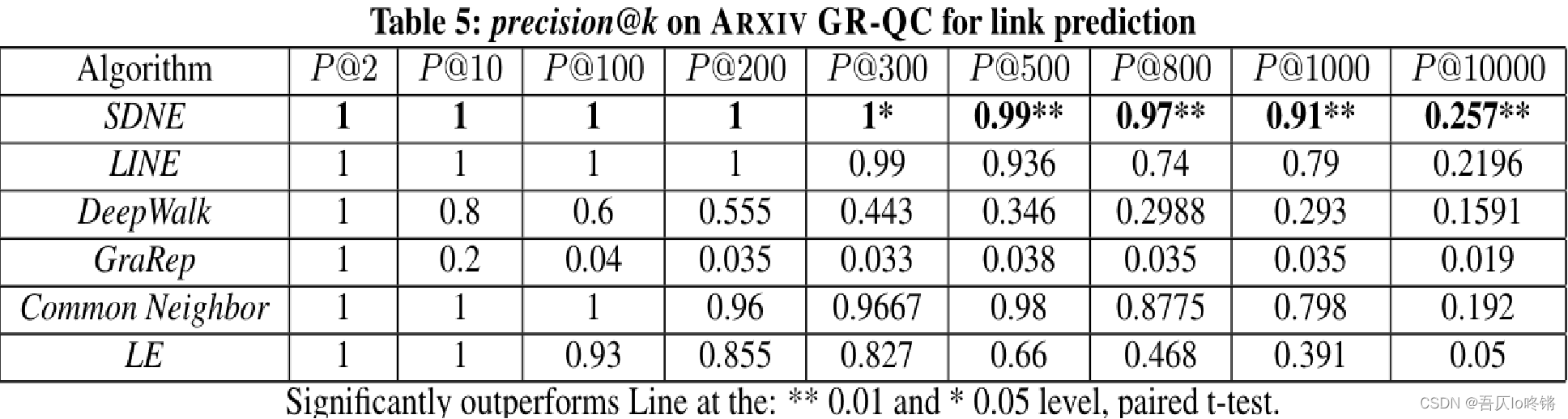
实验中，SDNE添加了共同邻居(Common Neighbor, CN)算法到链路预测实验中，但是具体权重和细节原文并没有透露。数据集方面，对ARXIV GR-QC数据集随机的隐藏了15%的边（约4000条边），然后KKK逐渐从2增加至10000，结果如下表格所示：

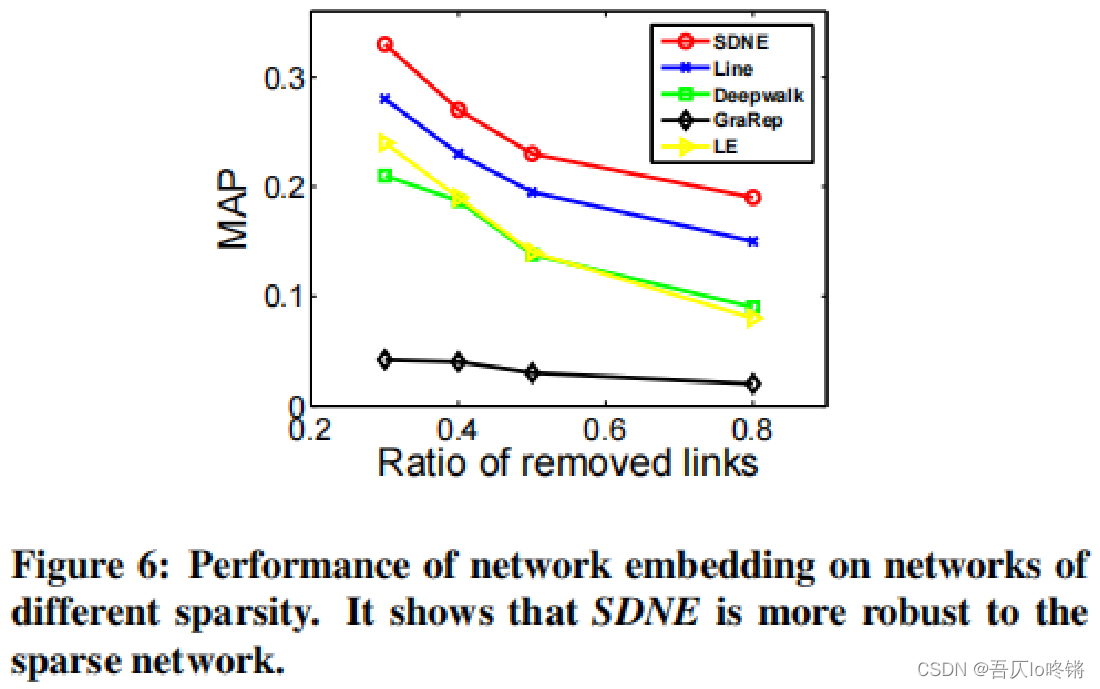
此外，还对不同稀疏性的数据集进行了实验，也就是对原数据集随机隐藏了更大比例的边，使得数据集变得稀疏。结果如下图所示：

分析：

• 随着KKK的增加，SDNE模型始终比其他图嵌入算法表现得更好。
• 当K=1000K=1000K=1000时，SDNE得准确率仍然高达0.9，而其他算法很快就掉到了0.8。
• 当图变稀疏时，SDNE(或LINE)与LE的差距变大。这表明了二阶临近度的重要性。
• 当隐藏掉图中80%的边后，SDNE模型仍比其他算法更好，表明了SDNE在稀疏网络上的有效性。

可视化

图嵌入中另一个重要的应用是将图可视化到一个二维空间中，使用学习到的低维嵌入向量作为可视化工具t-SNE的输入。

使用20-NEWSGROUP数据集，每个节点表示一个文档，每个文档都被标记为不同的分类，使用不同的颜色来划分相关的点。然后使用KL散度(Kullback-Leibler)来作为评价指标，KL越低则表明概率分布越接近，可视化结果越好。

实验结果如下所示：

分析：

• 对于LINE，虽然形成了不同类别的集群，但是不同类别文档的中心仍然混合在一起，如图7(b)。
• 对于GraRep，结果看起来更好，相同颜色的点形成了分段的组，但是不同组之间的边界并不是非常清晰。
  对于SDNE，显然在集群分类和边界方面都表现得最好，表明了SDNE在可视化任务中的优越性。

参数敏感性

在ARXIV-GRQC数据集上，SDNE对嵌入维度、α\alphaα和β\betaβ的取值进行了实验，结果如下所示：

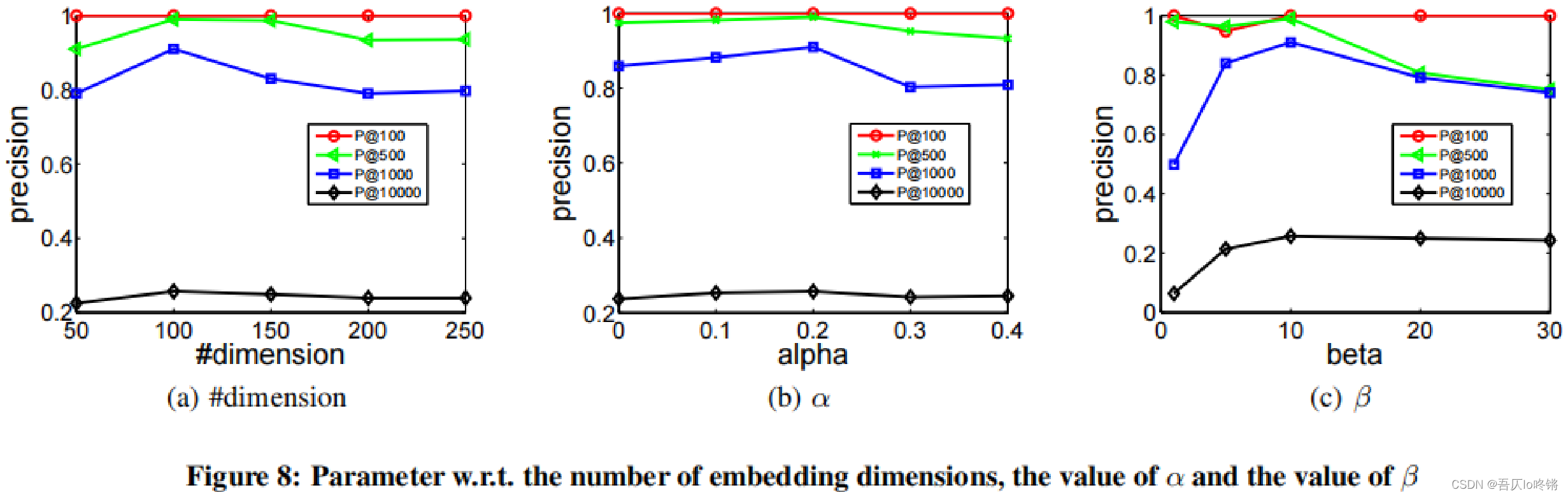
分析：

• 如图8(a)，SDNE模型对于嵌入向量的维度并不是非常敏感。
• 如图8(b)，α=0\alpha=0α=0表示不考虑一阶临近度，随着α\alphaα的增加，结果也有所提高。再次表明了一阶临近度和二阶临近度的有效性。
• 如图8©，β=0\beta=0β=0表示只考虑零元素，β=1\beta=1β=1表示零元素和非零元素的权重相同，随着β\betaβ的增加，给予非零元素更多的权重，使模型更关注重建非零元素。结果表明了应更多关注非零元素但不能只完全关注非零元素。

总结

文章提出了结构化深度图嵌入，称为SDNE，可以捕获高度非线性图结构。设计了一个半监督深度模型，采用了多层的自编码器。通过联合优化一阶临近度和二阶临近度，保留了图的局部和全局特征。实验结果现实在图重建、多标签分类、链路预测、可视化任务上取得了更优效果。

原文作者下一步工作将关注出现新节点的情况，也就是和当前节点没有链路的节点。

个人角度研读，水平有限，更多细节请移步原文。

原创不易，请勿转载（本不富裕的访问量雪上加霜 ）
博主首页：https://wzlodq.blog.csdn.net/
来都来了，不评论两句吗👀
如果文章对你有帮助，记得一键三连❤