树状数组（区间维护/单点修改）
创始人
2025-06-01 20:45:24
0次

1，定义

数组数组用于维护区间信息，简洁的几行的代码可以单点操作/区间查询，或者区间操作与单点查询。

虽然功能小于线段树，但是在相同功能的实现上，两者复杂度差不多。线段树

2，实现思路

树状数组有两个功能，一个是单点修改，区间（单点）查询。一个是区间修改，但是只能单点查询。两个功能不能同时使用。

我们先介绍第一个功能

先看一下树状数组的图

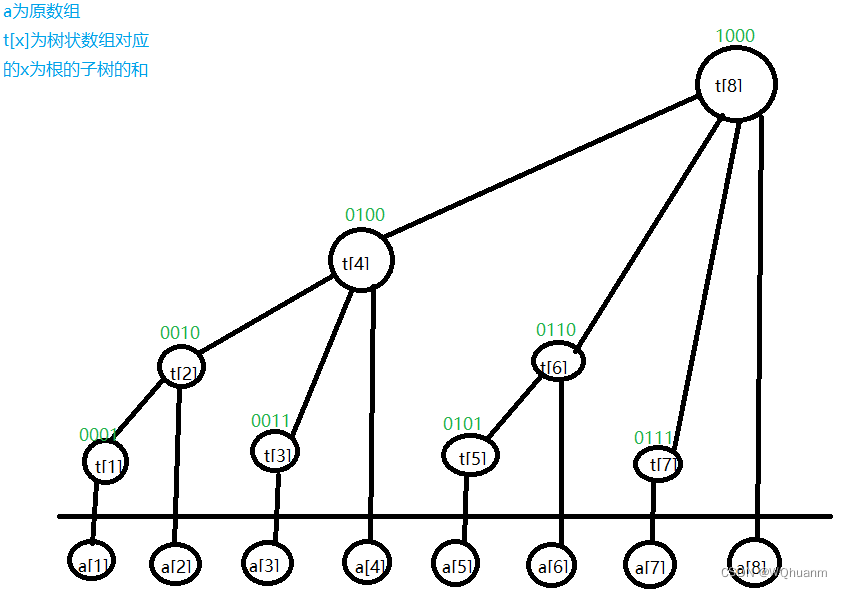
 我们观察出他的几个性质：

  1. 最外层的t是2的倍数（只有一个1），而且他的t[x]的值是a[1]+...+a[x]
  2. 每个点的父亲都是该点加上自己的最低位1就可得到如0010，最低位是10，0010+10=0100，就是父亲。
  3. 我们求x的1到x的前缀和，假设x=7，那么sum[7]=t[7]+t[6]+t[4],发现每次都是不断减去最低位1，直到最外层，即7-lowbit(7)=6,   6-lowbit(6)=4。

我们如何求最低位1呢？

  1. 我们知道：-x等价于x取反+1,假设x=10110，~x=01001,~x+1=01110。注意到-x与x的最低位1同位，其他高位全部不同，这是偶然吗？
  2. 我们对x取反，那么~x与x所有位不同，但是加上1后，再遇到最低位第一个0前，1全部变成0，不断往前推进（使得本来不同变得相同），当遇到0后，1被0吸收变成1，不再往后了，那么后面的高位仍然保持所有位不同。这样，我们把-x&x得到的就是lowbit，即最低位1

1，单点操作如何如何区间值更新呢

假如我们对x+k，那么他的祖先们都需要，去祖先的更新方法就是+lowbit

void add(int x,int k)
{for (int i=x; i<=n; i+=i&-i)t[i]+=k;
}

2，区间查询思路简单，我们t表示的是子树的值

那么我们从t[x]一直减最低位1，累加到t[0]即可

ll ask(int x)
{ll ans=0;for (int i=x; i; i-=i&-i)ans+=t[i];return ans;
}

模板题：P3374 【模板】树状数组 1

#include 
using namespace std;
#define ll     long long
const int N = 5e5 + 10;
int a[N],t[N];
int n;
void add(int x,int k)
{for (int i=x; i<=n; i+=i&-i)t[i]+=k;
}ll ask(int x)
{ll ans=0;for (int i=x; i; i-=i&-i)ans+=t[i];return ans;
}int main()
{int m,p,x,y;cin>>n>>m;for (int i=1; i<=n; ++i)cin>>a[i],add(i,a[i]);while (m--){cin>>p>>x>>y;if (p==1){add(x,y);}else if (p==2){cout<

实现功能2

  1. 我们这时只维护单点的值，不再是区间值，所以思路是把原来的数组表示为差分数组，那么原来的x的前缀和就成为x的值

代码没什么区别

int b[N];
int n;
void add(int x,int k)
{for (int i=x; i<=n; i+=i&-i)b[i]+=k;
}
ll ask(int x)
{ll ans=0;for (int i=x; i; i-=i&-i)ans+=b[i];return ans;
}

模板题2：P3368 【模板】树状数组 2

#include 
using namespace std;
#define ll long long
const int N = 5e5 + 10;int b[N];
int n;
void add(int x,int k)
{for (int i=x; i<=n; i+=i&-i)b[i]+=k;
}
ll ask(int x)
{ll ans=0;for (int i=x; i; i-=i&-i)ans+=b[i];return ans;
}int main()
{int m,p,x,y,k;cin>>n>>m;for (int i=1; i<=n; ++i)cin>>x,add(i,x),add(i+1,-x);while (m--){cin>>p;if (p==1){cin>>x>>y>>k;add(x,k),add(y+1,-k);}else if (p==2){cin>>x;cout<

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：Junit4 + Mockito进行单元测试实战案例

下一篇：Linux命令_lsof 网络/文件监控

相关内容

热门资讯

中央定调“能源强国”，核电板块... 12月15日，A股核电概念再度上涨，成分股天力复合（920576）上涨13.58%，雪人集团（002...
募资约61亿！深蓝汽车拟增资扩... 12月13日，长安汽车发布公告称，为满足业务发展和资金需求，长安汽车之控股子公司深蓝汽车科技有限公司...
优必选、越疆机器人入选“港交所... 新京报贝壳财经讯（记者韦博雅）12月14日和15日，优必选、越疆机器人分别宣布入选香港交易所推出的“...
一天三套豪宅！中国炒房客“带飞... 越南楼市，彻底疯了！最近，胡志明市一个楼盘开盘的清晨，仿佛让人看到了2015年上海内环楼市开盘现场的...
又要诞生一个“上纬新材”？ 这世上本没有路，走的人多了，便就成了路——这个道理在资本市场上也说得通。继智元机器人入主上纬新材和中...
破局“内卷”开拓蓝海——企业界... 文｜《中国企业家》记者 马吉英见习记者张昊编辑｜李会头图来源｜视觉中国“低价低质的恶性竞争，正在卷死...
中源家居上演“天地板” 新京报贝壳财经讯 12月15日，中源家居盘中一度跌停，上演“天地板”，成交额超5.9亿元。中源家居此...
罗永浩炮轰千元酒店祸害不明真相... 01.豆包手机助手回应「能截屏银行安全键盘」02.Reddit起诉澳大利亚青少年“社媒禁令”03.O...
新农合涨到400元，农民断缴背... 解决新农合断缴问题的根本，不在于村干部的催缴手段有多硬，而在于制度设计上，是否足够人性化，是否真正回...
陈天桥最新撰文：系统的融化，从... 我们在旧结构上越是用力地“加AI”，就越有可能是在给那些本该被淘汰的系统续命。文｜陈天桥盛大集团创始...