有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

动态规划五部曲：

1. 确定dp数组以及下标的含义

使用二维数组，即dp[i][j] 表示从下标为[0-i]的物品里任意取，放进容量为j的背包，价值总和最大是多少。

2. 确定递推公式

不放物品i：
由dp[i - 1][j]推出，即背包容量为j，里面不放物品 i 的最大价值，
此时dp[i][j]就是dp[i - 1][j]。
(当物品i的重量大于背包 j 的重量时，物品 i 无法放进背包中，背包内的价值依然和前面相同。)

放物品i：
由dp[i -1][j - weight[i]]推出，dp[i - 1][j - weight[i]] 为
背包容量为j -weight[i]的时候不放物品i的最大价值，
dp[i - 1][j - weight[i]] + value[i]（物品i的价值），背包表示放物品i得到的最大价值 。

所以递归公式： dp[i][j] = max(dp[i - 1][j], dp[i -1][j - weight[i]] + value[i]);

3. dp数组如何初始化

从dp[i][j]的定义出发，如果背包容量j为0的话，即dp[i][0]，无论是选取哪些物品，背包价值总和一定为0。
状态转移方程 dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); 可以看出i 是由 i-1 推导出来，那么i为0的时候就一定要初始化。
dp[0][j]，即：i为0，存放编号0的物品的时候，各个容量的背包所能存放的最大价值。

• 当 j < weight[0]的时候，dp[0][j] 应该是 0，因为背包容量比编号0的物品重量还小。
• 当j >= weight[0]时，dp[0][j] 应该是value[0]，因为背包容量放足够放编号0物品。

代码初始化如下：

for (int j = 0 ; j < weight[0]; j++) {  // 如果把dp数组预先初始化为0了，这一步就可以省略。dp[0][j] = 0;
}
// 正序遍历
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}

其他下标初始化
都可！初始化为0更方便

// 初始化 dp
vector> dp(weight.size(), vector(bagweight + 1, 0));
for (int j = weight[0]; j <= bagweight; j++) {dp[0][j] = value[0];
}

4. 确定遍历顺序
   都可
5. 举例推导dp
   

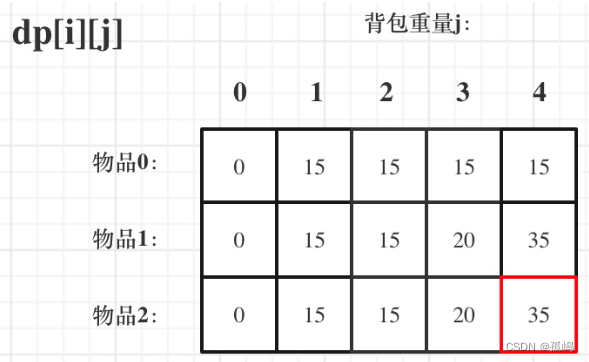
#include 
#include 
#include 
using namespace std;
void bagQues(){vector weight = {1,3,4};vector value = {15,20,30};int bagweight = 4;vector> dp(weight.size(),vector(bagweight+1,0));for (int j = weight[0]; j <= bagweight; ++j) {//初始化dp[0][j] = value[0];}for (int i = 1; i < weight.size(); ++i) {for (int j = 0; j <= bagweight; ++j) {if (j < weight[i]) dp[i][j] = dp[i-1][j];else dp[i][j] = max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);}}cout<bagQues();return 0;
}