Apollo控制部分3-- 车辆动力学模型详解
Apollo控制部分3-- 车辆动力学模型详解
- 摘要
- 一、预备知识
- 二、轮胎坐标系
- 三、车辆自行车模型公式推导
- 四、参考路径误差模型
@author:Wutong
@time:2023-03-17 20:05
摘要
动力学模型分析是整个无人车控制模块的基础,同时也是动力学模型是否准确也直接影响控制模块的精度。Apollo横向控制LQR和MPC算法中均需要汽车动力学模型进行控制量计算,所以我对这部分资料进行了整理记录。
本文主要参考了《汽车学》和《车辆动力学控制》两本书籍。首先介绍了车辆的轮胎坐标系模型,明确参考系的正方向,描述侧偏力、侧偏角以及侧偏刚度之间的关系;之后,计算推导车辆二自由度模型中横向加速度、横摆角加速度与轮胎转角之间得状态空间方程;最后,由二自由度模型计算车辆与参考路径的横向误差以及航向角误差,推导出其状态空间方程。
动力学模型只是为控制模块打基础,之后会继续更新Apollo控制模块的内容。
一、预备知识
参考书籍:
《高等学校教材:汽车学》
《车辆动力学控制(美)拉贾马尼著》
需要资源或者有任何问题可直接私信我。
二、轮胎坐标系
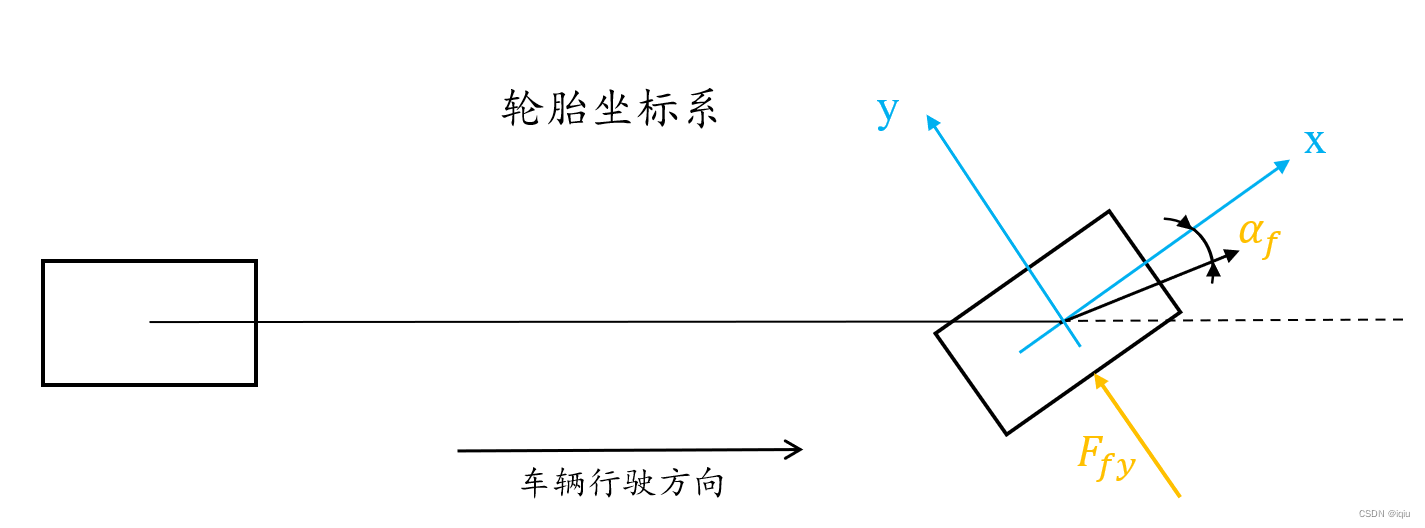
如图所示,车辆从左至右行驶。轮胎坐标系定义为:沿着行驶方向为xxx轴正方向,左侧垂直于行驶方向为yyy轴正方向。
图中FfyF_{fy}Ffy为侧偏力,即地面对轮胎的作用力,根据坐标系可知方向为正;车体通过车轴对轮胎的作用力与侧偏力方向相反。轮胎受上述两个力的作用会产生负的侧偏角,具体侧偏角分析过程可参考《汽车学》第一章第二节。
侧偏力公式 为:F=CαF=C \alphaF=Cα
其中F为侧偏力,C为侧偏刚度系数,α\alphaα为侧偏角。
根据轮胎坐标系有关符号定义可知,正的侧偏力产生负的侧偏角,因此侧偏刚度为负值。不同坐标系的定义可能不同,Apollo中侧偏刚度系数为正值,相应的状态方程也会有所改变,状态方程一般只会有正负号得差别,大家看到相应公式注意一下就行。
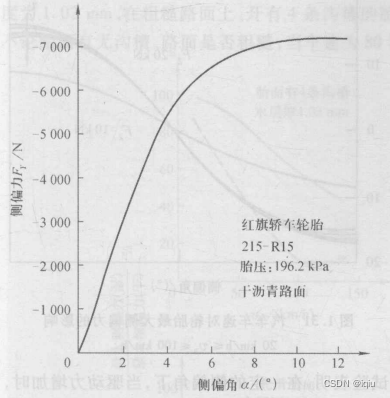
汽车正常行驶时,侧向加速度不超过0.4g,侧偏角不超过4°~5°,可以近似认为侧偏角与侧偏力呈线性关系。轮胎的侧偏特性曲线在α=0°\alpha=0°α=0°处的斜率称为侧偏刚度,单位为N/rad 。
小型轿车轮胎的侧偏刚度在(-28000 ~ -80000)N/rad范围内。侧偏刚度是决定操纵稳定性的重要轮胎参数。
三、车辆自行车模型公式推导
| 参数名称 | 符号 |
|---|---|
| 质量 | mmm |
| 横向速度 | vvv |
| 纵向速度 | uuu |
| 横摆角(航向角) | φ\varphiφ |
| 横摆角速度 | φ˙\dot{\varphi}φ˙ |
| z轴转动惯量 | IzI_{z}Iz |
| 前轮转角 | δ\deltaδ |
| 前/后轮胎沿x轴的力 | Fxf/FxrF_{xf} / F_{xr}Fxf/Fxr |
| 前/后轮胎沿y轴的力 | Fyf/FyrF_{yf} / F_{yr}Fyf/Fyr |
| 前后轮胎侧偏角 | αf/αr\alpha_{f} / \alpha_{r}αf/αr |
| 前后轮胎侧偏刚度 | Cf/CrC_{f} / C_{r}Cf/Cr |
| 前后轴到质心距离 | Lf/LrL_{f} / L_{r}Lf/Lr |
| 轴距 | L |
| 质心侧偏角 | β\betaβ |
将车辆简化为线性二自由度的自行车模型。不考虑方向盘等转向系统的影响,忽略方向盘的转动与前轮转角的关系,直接以前轮转角作为模型的输入;不考虑地面重构单元运动过程中悬架系统的影响,忽略z方向的运动以及俯仰运动和侧倾运动。
假定特定条件下沿x轴的纵向速度不变,据此车辆只有沿y轴的侧向运动和绕z轴横摆运动两个自由度,并且地面重构单元的轮胎的侧偏刚度在线性范围内;忽略驱动力对于轮胎侧偏特性的影响以及空气阻力,并且忽略轮胎回正力矩。将车辆坐标系的原点设在质心处,因为将质心设为原点那么车辆的转动惯量等质量分布参数对于质心坐标系来说是个常值,此时将车辆的绝对加速度与绝对角加速度以及外力与外力矩沿质心坐标系的轴线分解,就可以列出汽车运动微分方程。

二自由度汽车在前轮转角为δ\deltaδ时,受到的外力和外力矩沿y轴的分量为:
∑FY=may=Fyfcosδ+Fyr∑MZ=Izφ¨=LfFyfcosδ−LrFyr(1)\begin{align} \sum F_{Y} =& ma_{y} &=& F_{yf}\cos \delta +F_{yr} \\ \sum M_{Z} =& I_{z}\ddot{\varphi } &=&L_{f} F_{yf}\cos \delta - L_{r} F_{yr} \end{align} \tag{1} ∑FY=∑MZ=mayIzφ¨==Fyfcosδ+FyrLfFyfcosδ−LrFyr(1)
当δ\deltaδ很小时,侧偏力公式 Fyf=Cfαf、Fyr=CrαrF_{yf}=C_{f} \alpha_{f} 、F_{yr}=C_{r} \alpha_{r}Fyf=Cfαf、Fyr=Crαr代入式(1)动力学公式
∑FY=may=Cfαf+Crαr∑MZ=Izφ¨=LfCfαf−LrCrαr(2)\begin{align} \sum F_{Y}=& ma_{y} &=& C_{f} \alpha_{f} +C_{r} \alpha_{r}\\ \sum M_{Z}=& I_{z}\ddot{\varphi } &=&L_{f} C_{f} \alpha_{f} - L_{r}C_{r} \alpha_{r} \end{align} \tag{2} ∑FY=∑MZ=mayIzφ¨==Cfαf+CrαrLfCfαf−LrCrαr(2)
由图1所示,汽车前、后轴中点的速度为u1u_{1}u1 、u2u_{2}u2 ,汽车质心的侧偏角为β\betaβ,β=v/u\beta= v/uβ=v/u。ξ\xiξ是u1u_{1}u1与xxx轴的夹角,其值为:
ξ=v+Lfφ˙u=β+Lfφ˙u\xi =\frac{v+L_{f}\dot{\varphi}}{u} =\beta +\frac{L_{f}\dot{\varphi}}{u} ξ=uv+Lfφ˙=β+uLfφ˙
根据坐标系的规定,前后轮侧偏角为:
Cf=−(δ−ξ)=β+Lfφ˙u−δCr=v−Lrφ˙u=β−Lrφ˙u(3)\begin{align} C_{f}&= -(\delta -\xi ) = \beta +\frac{L_{f}\dot{\varphi}}{u}-\delta \\ C_{r}&=\frac{v-L_{r}\dot{\varphi}}{u}=\beta -\frac{L_{r}\dot{\varphi}}{u} \end{align} \tag{3} CfCr=−(δ−ξ)=β+uLfφ˙−δ=uv−Lrφ˙=β−uLrφ˙(3)
接下来利用固结于汽车上的车辆坐标系分析车辆横向加速度aya_{y}ay与横向速度vvv、纵向速度uuu和横摆角速度φ˙\dot{\varphi}φ˙之间的关系。如下图所示,OyO_{y}Oy和OxO_{x}Ox为车辆坐标系的纵轴和横轴,质心速度于ttt时刻在OxO_{x}Ox轴的分量为uuu,在OyO_{y}Oy轴上分量为vvv,车辆在水平路面上的行驶运动均可分解为质心的平移运动和绕质心的转动。
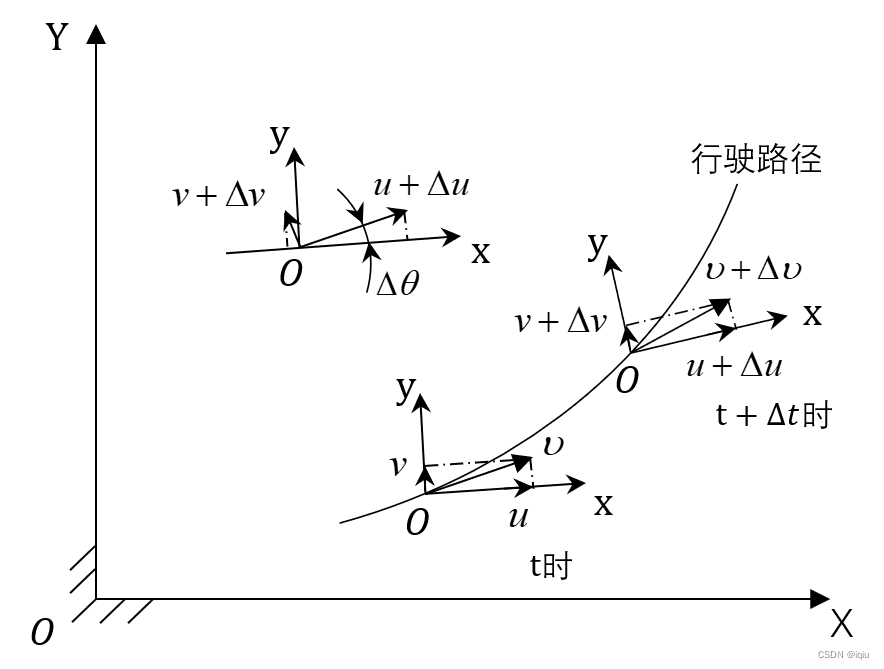
在t+∆tt+∆tt+∆t时刻,车辆坐标系中质心速度的大小与方向均发生变化,而车辆坐标系的纵轴与横轴的方向也发生变化。在计算质心处的加速度时,以ttt时刻的车辆坐标系作为参考坐标系,此时车辆沿OyO_{y}Oy轴速度分量变化为:
(v+Δv)cosΔθ−v+(u+Δu)sinΔθ=vcosΔθ+ΔvcosΔθ−v+usinΔθ+ΔusinΔθ\begin{array}{l} (v+\Delta v) \cos \Delta \theta-v+(u+\Delta u) \sin \Delta \theta \\ =v \cos \Delta \theta+\Delta v \cos \Delta \theta-v+u \sin \Delta \theta+\Delta u \sin \Delta \theta \end{array} (v+Δv)cosΔθ−v+(u+Δu)sinΔθ=vcosΔθ+ΔvcosΔθ−v+usinΔθ+ΔusinΔθ
考虑到Δθ\Delta \thetaΔθ很小,则sinΔθ≈Δθ,cosΔθ≈1\sin \Delta\theta \approx \Delta\theta,\cos\Delta \theta \approx 1sinΔθ≈Δθ,cosΔθ≈1,并略去二阶小量,上式变成:Δv+uΔθ\Delta v+u\Delta \thetaΔv+uΔθ
把上式除以∆t并取极限,可以得到质心加速度在ttt时刻车辆坐标系的yyy轴上的分量为:
ay=dvdt+udθdt=v˙+uφ˙(4)\begin{align} a_{y} = \frac{dv}{dt}+u \frac{d\theta }{dt}=\dot{v} +u\dot{\varphi } \end{align} \tag{4} ay=dtdv+udtdθ=v˙+uφ˙(4)
将式(3)、式(4)代入式(2)得到二自由度汽车运动微分方程式:
vu(Cf+Cr)+1u(LfCf−LrCr)φ˙−Cfδ=m(v˙+uφ˙)vu(LfCf−LrCr)+1u(Lf2Cf+Lr2Cr)φ˙−LfCfδ=Izφ¨(5)\begin{align} \frac{v}{u}(C_{f}+C_{r}) +\frac{1}{u} (L_{f} C_{f}-L_{r}C_{r})\dot{\varphi } -C_{f}\delta =m(\dot{v}+u\dot{\varphi } ) \\ \frac{v}{u}(L_{f} C_{f}-L_{r}C_{r})+\frac{1}{u} (L_{f}^{2} C_{f}+L_{r}^{2} C_{r})\dot{\varphi }-L_{f}C_{f}\delta=I_{z}\ddot{\varphi } \end{align} \tag{5} uv(Cf+Cr)+u1(LfCf−LrCr)φ˙−Cfδ=m(v˙+uφ˙)uv(LfCf−LrCr)+u1(Lf2Cf+Lr2Cr)φ˙−LfCfδ=Izφ¨(5)
将β=v/u\beta= v/uβ=v/u代入式(5),并将其中y¨=ay=v˙+uφ˙,y˙=v\ddot{y}=a_{y}=\dot{v}+u\dot{\varphi} , \dot{y}=vy¨=ay=v˙+uφ˙,y˙=v进行符号替代,可得:
注意,这里设置y¨=ay=v˙+uφ˙\ddot{y}=a_{y}=\dot{v}+u\dot{\varphi}y¨=ay=v˙+uφ˙,官方版本是y¨=v˙\ddot{y}=\dot{v}y¨=v˙,所以推导出的状态空间方程有一项不一样
y¨=Cf+Crmuy˙+LfCf−LrCrmuφ˙−Cfmδφ¨=LfCf−LrCrIzuy˙+Lf2Cf+Lr2CrIzuφ˙−LfCfIzδ(6)\begin{align} \ddot{y}&=\frac{C_{f}+C_{r}}{mu} \dot{y} +\frac{ L_{f} C_{f}-L_{r}C_{r}}{mu}\dot{\varphi } -\frac{ C_{f}}{m}\delta \\ \ddot{\varphi }&= \frac{L_{f} C_{f}-L_{r}C_{r}}{I_{z}u} \dot{y} +\frac{L_{f}^{2} C_{f}+L_{r}^{2} C_{r}}{I_{z}u} \dot{\varphi }-\frac{L_{f}C_{f}}{ I_{z}}\delta \end{align} \tag{6} y¨φ¨=muCf+Cry˙+muLfCf−LrCrφ˙−mCfδ=IzuLfCf−LrCry˙+IzuLf2Cf+Lr2Crφ˙−IzLfCfδ(6)
将式(6)整理,可得二自由度模型状态空间方程,即横向加速度、横摆角加速度与轮胎转角之间的关系:
ddt[yy˙φφ˙]=[01000Cf+Crmu0Lf∗Cf−Lr∗Crmu00010Lf∗Cf−Lr∗CrIzu0Lf2∗Cf+Lr2∗CrIzu][yy˙φφ˙]+[0−Cfm0−Lf∗CfIz]δ(7)\begin{align} \frac{d}{dt} \begin{bmatrix} y \\ \dot{y} \\ \varphi \\ \dot{\varphi } \end{bmatrix}= \begin{bmatrix} 0 & 1 & 0 & 0\\ 0 & \frac{C_{f}+ C_{r}}{m u} & 0 & \frac{L_{f}*C_{f}-L_{r}*C_{r} }{m u}\\ 0 & 0 & 0 & 1\\ 0 & \frac{L_{f}*C_{f}-L_{r}*C_{r} }{I_{z} u} & 0 & \frac{L_{f}^{2} *C_{f}+L_{r}^{2}*C_{r}}{I_{z}u} \end{bmatrix}\begin{bmatrix} y \\ \dot{y} \\ \varphi \\ \dot{\varphi } \end{bmatrix}+\begin{bmatrix} 0 \\ -\frac{C_{f}}{m} \\ 0 \\ -\frac{L_{f}*C_{f}}{I_{z}} \end{bmatrix} \delta \end{align} \tag{7} dtdyy˙φφ˙=00001muCf+Cr0IzuLf∗Cf−Lr∗Cr00000muLf∗Cf−Lr∗Cr1IzuLf2∗Cf+Lr2∗Cryy˙φφ˙+0−mCf0−IzLf∗Cfδ(7)
四、参考路径误差模型
参考书籍:车辆动力学控制(美)拉贾马尼著(推导过程中书中式(2.43)有误,注意甄别)
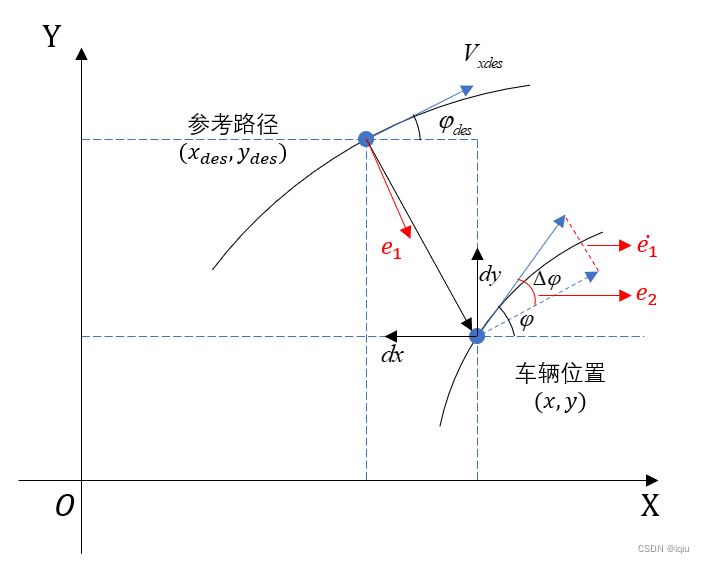
定义e1e_{1}e1为横向误差,车辆质心距车道中心线的距离,e2e_{2}e2为航向角误差,车辆转弯半径为R。此路径点对应的期望横摆角速度和期望横向加速度可以由纵向速度和转弯半径求得:
φ˙des=uRaydes=u2R=uφ˙des(8)\begin{align} \dot{\varphi} _{des}&=\frac{u}{R} \\ a_{ydes}&=\frac{u^{2} }{R}= u \dot{\varphi} _{des} \end{align} \tag{8} φ˙desaydes=Ru=Ru2=uφ˙des(8)
定义
e1¨=ay−aydes=(v˙+uφ˙)−u2R=v˙+u(φ˙−φ˙des)e2=φ−φdes(9)\begin{align} \ddot{e_{1}}&=a_{y}-a_{ydes}=(\dot{v}+u\dot{\varphi })-\frac{u^{2} }{R} = \dot{v}+u(\dot{\varphi }-\dot{\varphi} _{des}) \\ e_{2}&=\varphi -\varphi _{des} \end{align} \tag{9} e1¨e2=ay−aydes=(v˙+uφ˙)−Ru2=v˙+u(φ˙−φ˙des)=φ−φdes(9)
假设纵向速度uuu为常数
e1=v+u(φ−φdes)(10)\begin{align} e_{1}&=v+u(\varphi -\varphi _{des}) \end{align} \tag{10} e1=v+u(φ−φdes)(10)
将式(8)(9)(10)代入式(5),消去变量vvv、φ˙\dot{\varphi}φ˙,得:
m(e1¨+aydes)=Cf+Cru(e1˙−ue2)+LfCf−LrCru(e2˙+φ˙des)−CfδIz(e2¨+φ¨des)=LfCf−LrCru(e1˙−ue2)+Lf2Cf+Lr2Cru(e2˙+φ˙des)−LfCfδm(\ddot{e_{1}}+a_{ydes} )=\frac{C_{f}+C_{r}}{u} (\dot{e_{1}}-ue_{2} )+\frac{L_{f} C_{f}-L_{r}C_{r}}{u} (\dot{e_{2}}+\dot{\varphi} _{des} )-C_{f}\delta \\ I_{z}(\ddot{e_{2}} +\ddot{\varphi}_{des} )=\frac{L_{f} C_{f}-L_{r}C_{r}}{u}(\dot{e_{1}}-ue_{2})+\frac{L_{f}^{2} C_{f}+L_{r}^{2} C_{r}}{u}(\dot{e_{2}}+\dot{\varphi} _{des} )-L_{f}C_{f}\delta m(e1¨+aydes)=uCf+Cr(e1˙−ue2)+uLfCf−LrCr(e2˙+φ˙des)−CfδIz(e2¨+φ¨des)=uLfCf−LrCr(e1˙−ue2)+uLf2Cf+Lr2Cr(e2˙+φ˙des)−LfCfδ
化简上式得:
e1¨=e1˙Cf+Crmu−e2Cf+Cru+e2˙LfCf−LrCrmu+φ˙des(LfCf−LrCrmu−u)−δCfme2¨=e1˙LfCf−LrCrIzu−e2LfCf−LrCrIz+e2˙Lf2Cf+Lr2CrIzu+φ˙desLf2Cf+Lr2CrIzu−δLfCfIz−φ¨des(11)\begin{align} \ddot{e_{1}}=&\dot{e_{1}}\frac{C_{f}+C_{r}}{mu} -e_{2}\frac{C_{f}+C_{r}}{u} \\ &+\dot{e_{2}}\frac{L_{f} C_{f}-L_{r}C_{r}}{mu}\\ &+\dot{\varphi}_{des}(\frac{L_{f} C_{f}-L_{r}C_{r}}{mu} -u) -\delta\frac{ C_{f}}{m}\\ \ddot{e_{2}} =&\dot{e_{1}}\frac{L_{f} C_{f}-L_{r}C_{r}}{I_{z}u}-e_{2}\frac{L_{f} C_{f}-L_{r}C_{r}}{I_{z}}\\ &+\dot{e_{2}}\frac{L_{f}^{2} C_{f}+L_{r}^{2} C_{r}}{I_{z}u}+\dot{\varphi} _{des}\frac{L_{f}^{2} C_{f}+L_{r}^{2} C_{r}}{I_{z}u}\\ &-\delta\frac{L_{f}C_{f}}{I_{z}}-\ddot{\varphi}_{des} \end{align} \tag{11} e1¨=e2¨=e1˙muCf+Cr−e2uCf+Cr+e2˙muLfCf−LrCr+φ˙des(muLfCf−LrCr−u)−δmCfe1˙IzuLfCf−LrCr−e2IzLfCf−LrCr+e2˙IzuLf2Cf+Lr2Cr+φ˙desIzuLf2Cf+Lr2Cr−δIzLfCf−φ¨des(11)
在实际计算中,忽略φ¨des\ddot{\varphi}_{des}φ¨des项,由此可得路径跟踪误差模型状态方程为式(12):
ddt[e1e1˙e2e2˙]=[01000Cf+Crmu−Cf+CruLfCf−LrCrmu00010LfCf−LrCrIzu−LfCf−LrCrIzLf2Cf+Lr2CrIzu][e1e1˙e2e2˙]+[0LfCf−LrCrmu−u0Lf2Cf+Lr2CrIzu]φ˙des+[0−Cfm0−LfCfIz]δ\frac{d}{dt}\begin{bmatrix} e_{1} \\ \dot{e_{1}} \\ e_{2} \\ \dot{e_{2}} \end{bmatrix} = \begin{bmatrix} 0 & 1 & 0 & 0\\ 0 & \frac{C_{f}+C_{r}}{mu} & -\frac{C_{f}+C_{r}}{u} & \frac{L_{f} C_{f}-L_{r}C_{r}}{mu}\\ 0 & 0 & 0 &1 \\ 0 & \frac{L_{f} C_{f}-L_{r}C_{r}}{I_{z}u} & -\frac{L_{f} C_{f}-L_{r}C_{r}}{I_{z}} & \frac{L_{f}^{2} C_{f}+L_{r}^{2} C_{r}}{I_{z}u} \end{bmatrix} \begin{bmatrix} e_{1} \\ \dot{e_{1}} \\ e_{2} \\ \dot{e_{2}} \end{bmatrix}+ \begin{bmatrix} 0 \\ \frac{L_{f} C_{f}-L_{r}C_{r}}{mu}-u \\ 0\\ \frac{L_{f}^{2} C_{f}+L_{r}^{2} C_{r}}{I_{z}u} \end{bmatrix}\dot{\varphi} _{des}+ \begin{bmatrix} 0 \\ -\frac{ C_{f}}{m} \\ 0 \\ -\frac{L_{f}C_{f}}{I_{z}} \end{bmatrix}\delta dtde1e1˙e2e2˙=00001muCf+Cr0IzuLfCf−LrCr0−uCf+Cr0−IzLfCf−LrCr0muLfCf−LrCr1IzuLf2Cf+Lr2Cre1e1˙e2e2˙+0muLfCf−LrCr−u0IzuLf2Cf+Lr2Crφ˙des+0−mCf0−IzLfCfδ
相对路面误差动力学模型公式总结如下:
| 参数名称 | 符号 | |
|---|---|---|
| 状态空间向量 | xxx | x=[e1e1˙e2e2˙]Tx=[e_{1}\quad \dot{e_{1}} \quad e_{2} \quad \dot{e_{2}}]^{T}x=[e1e1˙e2e2˙]T |
| x˙=Ax+Bφ˙des+Cδ\dot{x}=Ax+B\dot{\varphi} _{des}+C\deltax˙=Ax+Bφ˙des+Cδ | ||
| 横向误差 | e1e_{1}e1 | |
| 航向角误差 | e2e_{2}e2 | |
| 前轮转向角 | δ\deltaδ | |
| 路径参考点理论横摆角速度 | φ˙des\dot{\varphi} _{des}φ˙des |
未完待续~~~
下一篇:Hadoop运行模块
